Active Math Posts


How To: Figure out the area of quadrilaterals
Quadrilaterals are four sided shapes that are closed. They are polygons. Quadrilaterals can be classified broadly in two ways. If the quadrilateral has a two pair of parallel sides then it falls in to the parallelogram category. Further now it can be broken down in to other shapes like square, rectangle, rhombus. If it has only one pair of parallel side then it falls into the trapezoid category. To compute the are of a trapezoid first you need to know the lengths of the parallel sides. Add th...

How To: Solve for x in the algebra equation -7 + 13x = 58
In this video he just explained about how to solve an algebra problem. The problem is -7+13x=58. He just solve the problem in simple steps. First you find out the x in this problem. To find out x you just add 7 to each side. Then it will be -7+7+13x=58+7. Then the equation will be 13x=65 because in the left side of the equation -7 canceled by +7 so then the equation is 13x=65. Next you just add the divide by 13 each side of the equation. Then the equation will be 13x/13=65/13. Then 13 divided...

How To: Reduce fractions to their simplest form in basic math
This video teaches us the method to simplify the fractions. Let us take an example of 18/24. Find a number that goes into both 18 and 24. Divide the top and bottom by the same number. Here, 2 will go into both numbers. So, the number now becomes (18/2)/(24/2) which gives 9/12. This fraction can be further simplified by dividing the top and bottom by 3. We get 3/4 which is our final answer. The fractions 18/24, 9/12 and 3/4 are called equivalent fractions since they are of the same size. Simil...

How To: Quickly find the area of a trapezoid
In this video, Mr. Maisonet provides a quick and easy method for calculating the area of a trapezoid. In the first step, The lengths of the two bases (the two sides of a trapezoid that are parallel to one another) are averaged. The lengths of the bases are first added together, and the sum is divided by two, yielding the average. The average is then multiplied by the height. The resulting product is the area of the trapezoid. This method for finding the area of a trapezoid is mathematically s...

How To: Reduce a fraction by finding common factors in math
The aim of the video is to show how to reduce a fraction by factoring out prime numbers that are common to both the numerator and the denominator. The example shown in the video is 27/21. The number 27 can be achieved by multiplying 3 by 9 and the number 21 is the result of 3 multiplied by 7. The common factor, therefore in both the numerator and the denominator is 3. 3 on the top divided by 3 on the bottom is 1 and so this can be removed without affecting the value of the fraction, leaving 9...
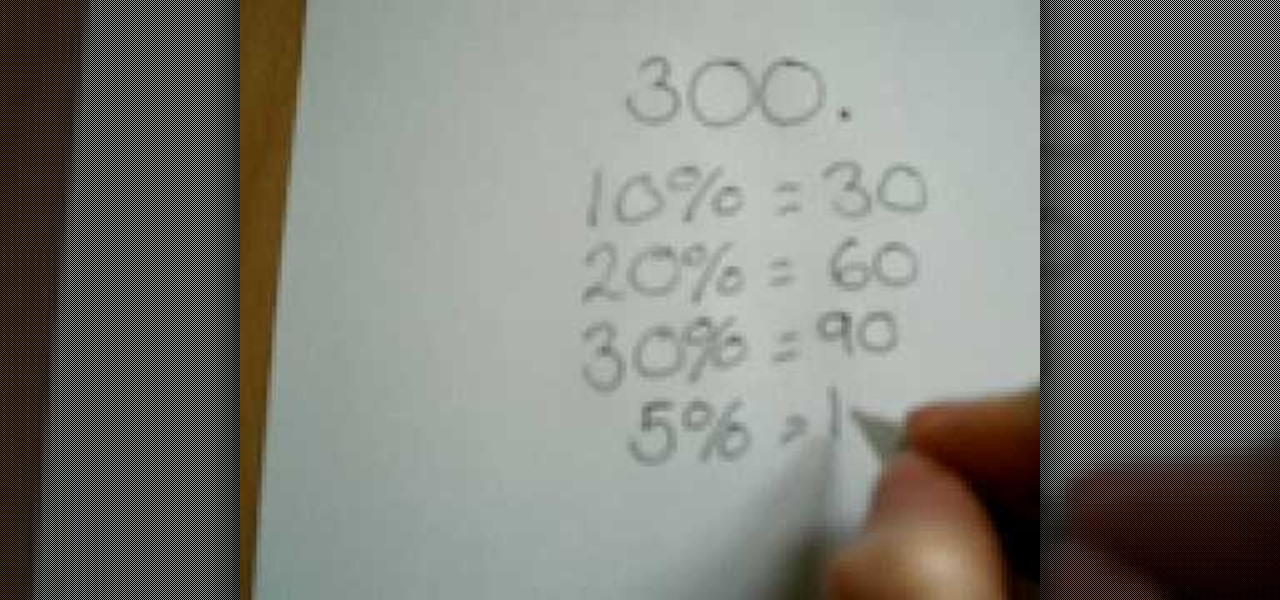
How To: Solve basic percentages
In this video tutorial, viewers learn how to work out basic percentages. The key is to always find 10% of the number first. To find 10%, divide the number by 10. It's very simple because you simply move one decimal to the left. Once you have found the 10%, you can simply find the next 10% by doubling the number. The other thing you can do is find 5% of the number by dividing the 10% number in half. This video will benefit those viewers who have trouble with find percentage or forgot how to an...

How To: Easily find the area of a rhombus
In this video, you will learn how to find the area of a rhombus. The formula is A = 1/2 d1 * d2. The d1 is the diagonal inside the rhombus, while d2 is the other diagonal inside the rhombus. You will need to find the length of these lines in order to complete the formula. For example, if one length is 5 and the other is 4, then you should plug in the numbers into the formula. This will equal 20 divided by 2, or 10. 10 units squared is the answer to this particular problem. Viewing this video ...

How To: Use cross products to solve proportions
To solve a proportion for a variable you should employ cross multiplication. The basis of cross multiplication is the property which states that the product of the numerator of one fraction and the denominator of what it is set equal to is equal to the product of the remaining denominator and numerator. For example if you have x/15=21/45 you simply need to multiply x by 45 and 15 by 21 then set them equal to each other. The result of this is 45x=315. To solve this new problem for x, divide bo...
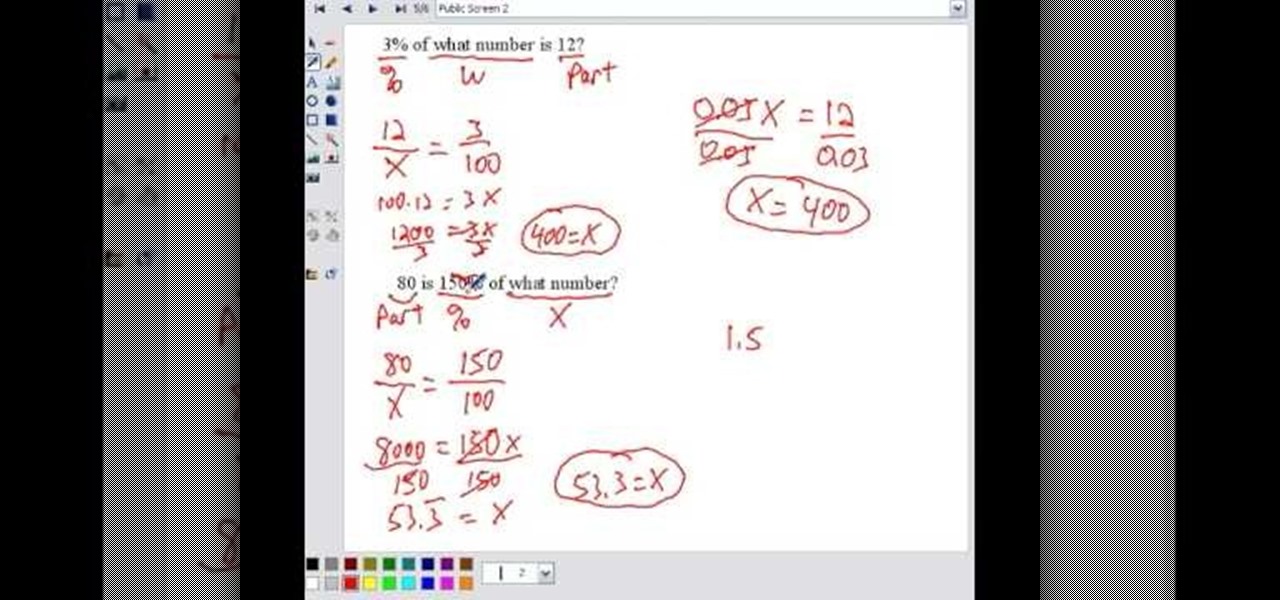
How To: Solve percent problems
Percent problems, also called as proportion problems, are simple problems where you deal with percentages. Given a percentage problem you may need to identify the percentage, the part or whole quantity from it. You can use the proportion or percent equation to do this. Proportion equations says that the ratio of part to the whole is equal to the ratio of percentage to one hundred. Percent equation says that the product of the percentage in the decimal form and the whole gives you the quantity...
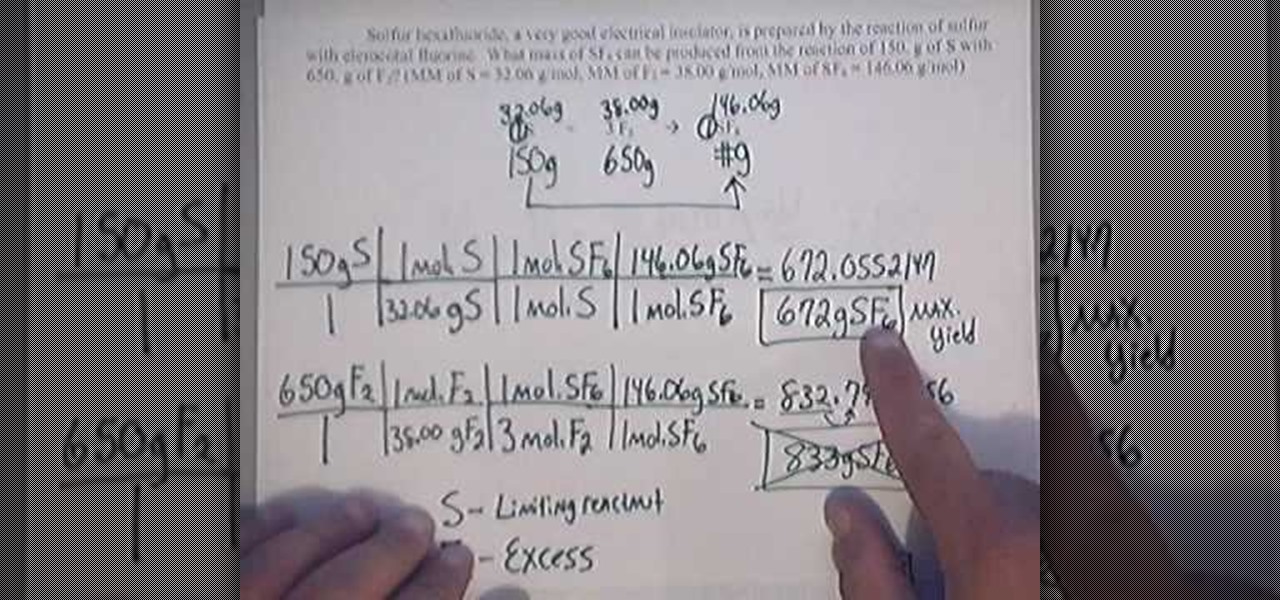
How To: Calculate percent yield
This video shows you how to calculate the percentage yield in chemistry. To find the percentage yield, you will need to divide the actual yield by the theoretical yield. Then, multiply it by 100: i.e. % yield = actual yield/theoretical yield x 100. An actual yield is the amount of a substance produced in an actual laboratory experiment. It is based on an actual physical measurement of a quantity. The theoretical yield is the yield as is calculated on paper: i.e. through calculations. Therefor...

How To: Interpret derivatives of marginal cost and revenue
This video tells us the method of interpreting derivatives of marginal cost and revenue. If C(x) is the cost of producing x units of a product, C(400) would be the cost to produce 400 units. Now marginal cost is the cost of producing one unit which is equal to the derivative of the cost function or C'(400) which is equal to limit of h tends to zero or lim h->0 [lim(400+h)-lim(400)]/h which is approximately equal to [lim(401)-lim(400)]/1. Similarly, if R(x) is your revenue function, marginal r...

How To: Simplify algebraic expressions with negative exponents
This video explains the process of simplifying an algebraic expression with negative exponents. The video starts with an example of such an algebraic expression; the expression contains negative powers in both the numerator and denominator. The location of the negative exponents is first pointed out visually. Next, it is observed that there are like based or variables in both the numerator and denominator; however, it is explained that the numerator must first be expanded before the expressio...
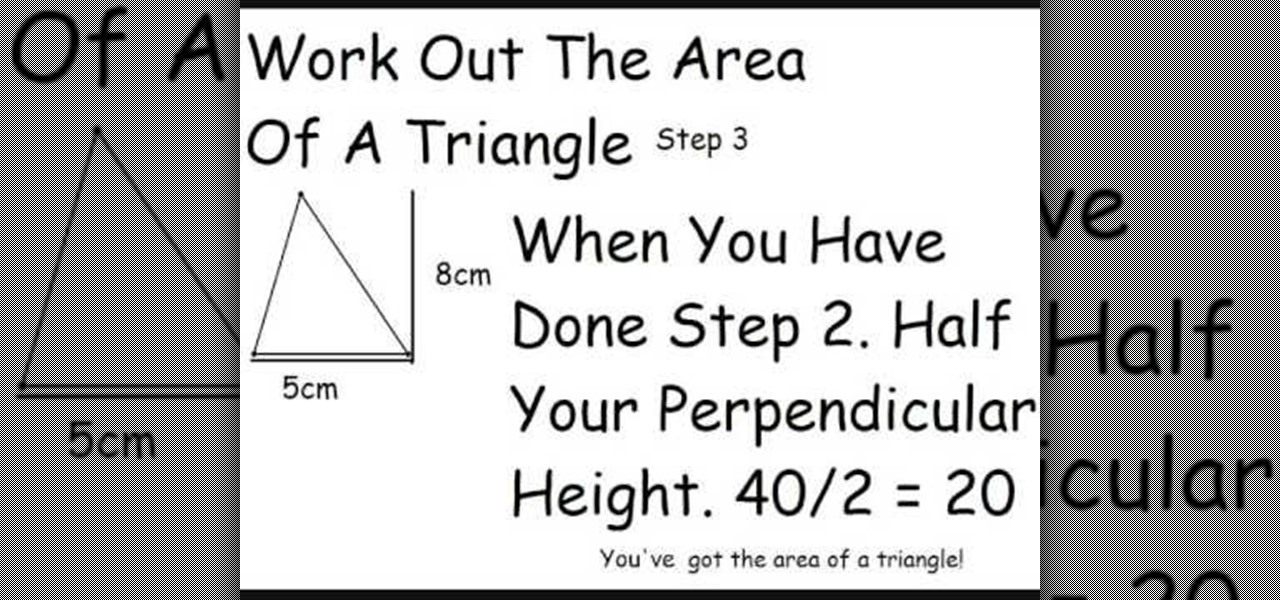
How To: Work out the area of a triangle and a parallelogram
This tutorial describes the method to calculate the area of a triangle and a parallelogram To calculate the area of a triangle:

How To: Prepare for the SAT math section
How to prepare for the math section of SAT:Eva for brightstorm2 gives us a few quick tips to solve the math section in the SAT test. They are simple, easy yet crucial to help you get through the math section. Let us begin with the basics. Basic are simple tips like read carefully, use your calculator wisely, use all the information given, do not worry about formulae and symbols, tackle the “always”, “never”, “must and “could and “can” problems. To explain them in detail; you should pay attent...

How To: Find the surface area of a basic cylinder
First of all cut of the top and the bottom of the cylinder to get two circles. Now take a scissors and cut of the cylinder into two halves from the top to the bottom as shown. Now you get a rectangle shape. You can easily measure the length of the cylinder but to measure the base is a problem. So mark a point on the table with tape and also make a mark on the can or the object you want to measure. Now place the two points over each other. Now use a ruler as a guide and move the can so that th...

How To: Use optimization methods in calculus
This video shows how to use optimization methods in calculus. Optimization means finding the maximum or minimum values of a quantity or finding when the maximum or minimum occurs.What quantities are optimized in economics?we want to minimize costs or maximize revenue.First steps in any optimization problem1.Identify the quantity to be optimized i.e., read the problem exactly what is exactly maximized or minimized.2.Identified the feasible domain. This is important because the math we can opti...

How To: Use proportions to solve application problems
In this video they are showing how to use proportions to solve word problems. In the first example they used 2/3 is equal to x/6. To solve for x, you begin by cross multiplying setting up and equation 3x=12. Next, divide 12 by 3 which equals 4. So x equals 4. In the next example, she has given a situation where she is making a ranch dip using a ranch powder and sour cream. She want to use 80oz of sour cream and she wants to know how much powder ranch she will need. She know that for 16oz of s...

How To: Calculate the weighted average of specific values
The way to convert 0.300 Moles of water into Grams is to start by writing what you have. Then put grams on top and moles on the bottom, then put one by the mole, the omler mass goes by grams. Now you figure out the moler mass of water which has 2 H and 1 O, its 2 times 1 which is the atomic mass for hydrogen plus 16.0 for oxygen which gives a total of 18.0 g/mol. So then you insert the 18 up by the grams, now you can cancel out the moles and multiply 0.300 times 18.0g and it gives you 5.40 g,...
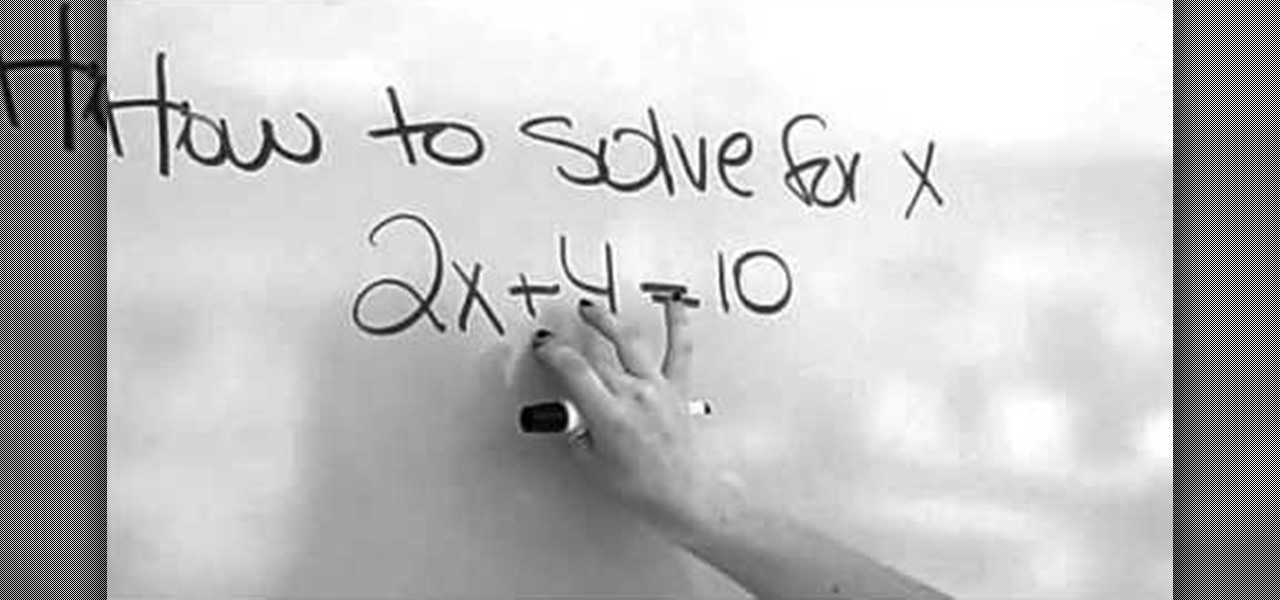
How To: Solve for X in algebra
This video demonstrates how to solve for X in algebra. The equation taken for this is 2X+4=10.The first thing you have to do to solve this equation is to get X by itself on one side of the equation. In order to do that you take the number that does not have X with it and do the opposite operation that has been done. So in the equation here we have plus four so we subtract four from both sides of the equation. What we do to one side of the equation has to be done to the other side of the equat...

How To: Convert a percentage to a decimal number
Learn how to easily convert percentage values into decimals in this quick video. When converting percentages it is important to remember that a percentage simply means to divide by 100. For example, take 5%. That means 5 divided by 100 or 0.05. These can easily be done on your calculator once you understand the meaning of percentage. Another example, let's take 23%. Divide 23 by 100 and you get .23. Finally, as a last example takes 99%. Take 99 divide it by 100 and the answer will come out to...
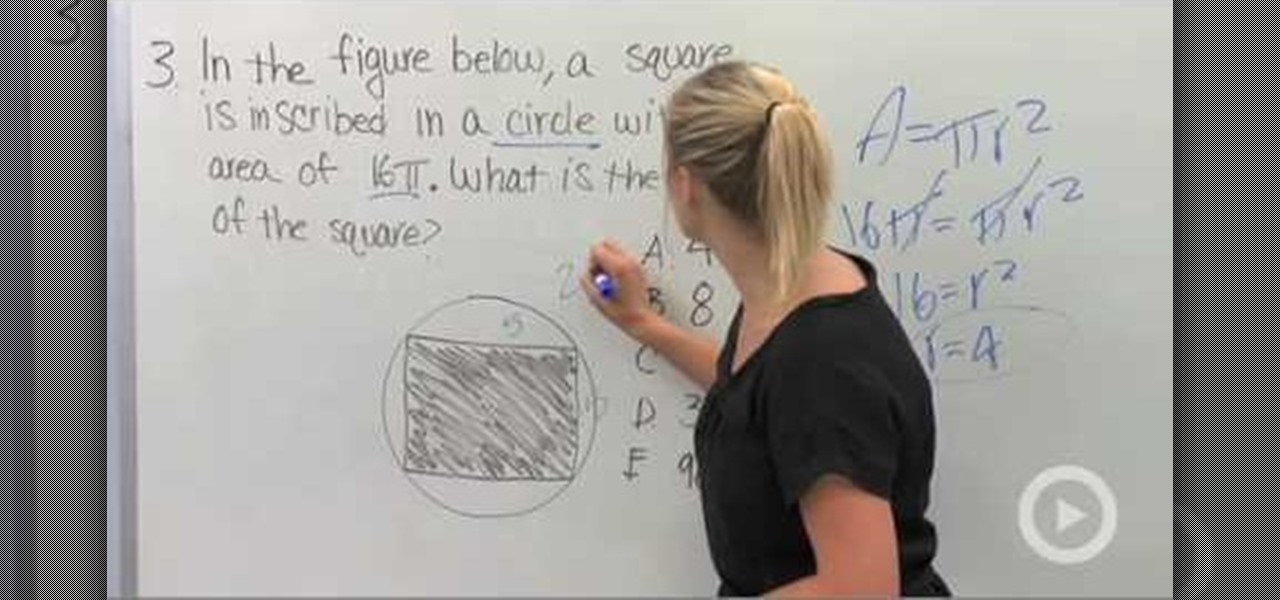
How To: Prepare for the PSAT math section
In this video the tutor explains a four strategies for standardize tests, complete with examples of each, explained fully. The first strategy to prepare for the math section of the PSAT, is simply reading the question, and understanding what the question is asking. The second strategy the tutor recommends is that, for some questions, you choose your own numbers. One more strategy suggested is to use the figures and diagrams. The final strategy shown in the video, is to "plug in answer choices...
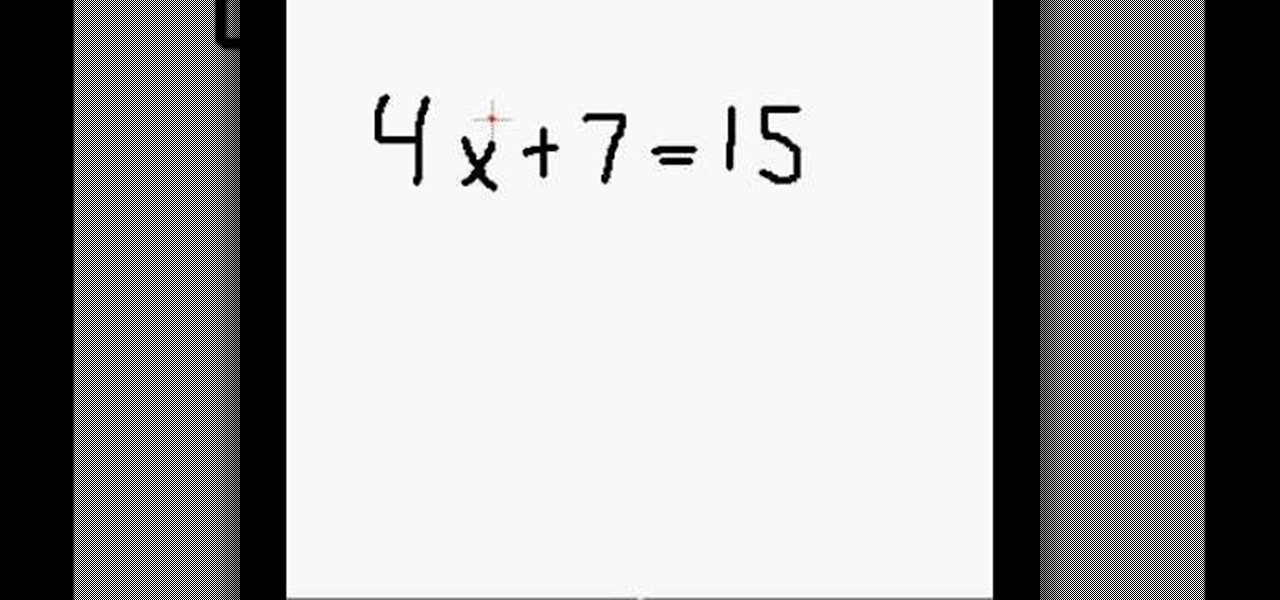
How To: Solving for "x" using multiplication and division
Solving for "x" using multiplication and divisionHere is a typical algebraic equation "2x=12". Multiplication in algebra will have the "x" next to a number. The process will be a combination of multiplication and division to solve for "x". To get "x" alone, we do the opposite operation. 2x/2=12/2. Bring down the "=". You must balance the equation to make sure you did the computation correctly. 2x6=12. Next, we have a multiplication and addition problem. 4x+7=15. We must get rid of the 7. +7-7...

How To: Solve an equations for x
This video demonstrates how to solve algebraic equations of the first degree for the variable, "X"; in other words, the variables contained in these equations are not raised to any power other than one, which is implicit. The video starts out with an example of such an algebraic equation. Before beginning to solve the equation, the video explains the meaning of the equals sign, the definition of an equation, and what a variable is. Next the video explains what is meaning by "solving for X". T...

How To: Solve a word problem that involves proportions
In this Education video tutorial you will learn how to solve a word problem that involves proportions. To solve such problems you got to express the scenario in proportions. For example, in the problem, ‘Jacob ran 10 miles in 80 minutes’; this rate can be expressed as 10miles/ 80 minutes. The second part of the problem is to find out ‘at that rate how far would he run in 2.5 hours’? ‘How far’ being a variable, write it as ‘x’ and this can be expressed as x/ 2.5 hours. So, the complete equatio...

How To: Define an antiderivative in calculus
The relationship and the definition of derivatives and anti-derivatives is described in this video. First, consider a function F(x)=x^3-5x+2 and another with small 'f', f(x)=3x-5. f(x) here is the derivative of F(x). However, on the contrary, F(x) is said to be the anti-derivative of f(x). There is a catch though; even though F(x) has only one derivative in the form of f(x), f(x) here has more than one anti-derivative. This is because f(x)'s anti-derivatives are of the form F(x)=x^3-5x+c, whe...

How To: Find the midpoint of a line segment
A good place to start when you want to learn how to find a midpoint of a line is a circle. Take the diameter of a circle, for instance if the coordinates of the starting point are (1,6) and the coordinates for the ending point are (11,6). The midpoint of a line is the exact central point where a line through these two points would meet. Now the value of y is a constant one as the line runs parallel to the x-axis, the value of x changes by 10, the half of which is 5, this is not the midpoint t...

How To: Use definite integrals to find the area of curves
Brightstorm explains how to use definite integrals to find area. There are two basic area problems: one in which the area lies between the function and the x-axis, and one where the area lies between the two functions. In the first case, if the curve lies above the x-axis for x=a to x=b, the definite integral returns the area. If it lies below the x-axis for x=a to x=b, then the definite integral returns a negative area. In the second case, we assume that f(x) is the higher curve and g(x) is ...
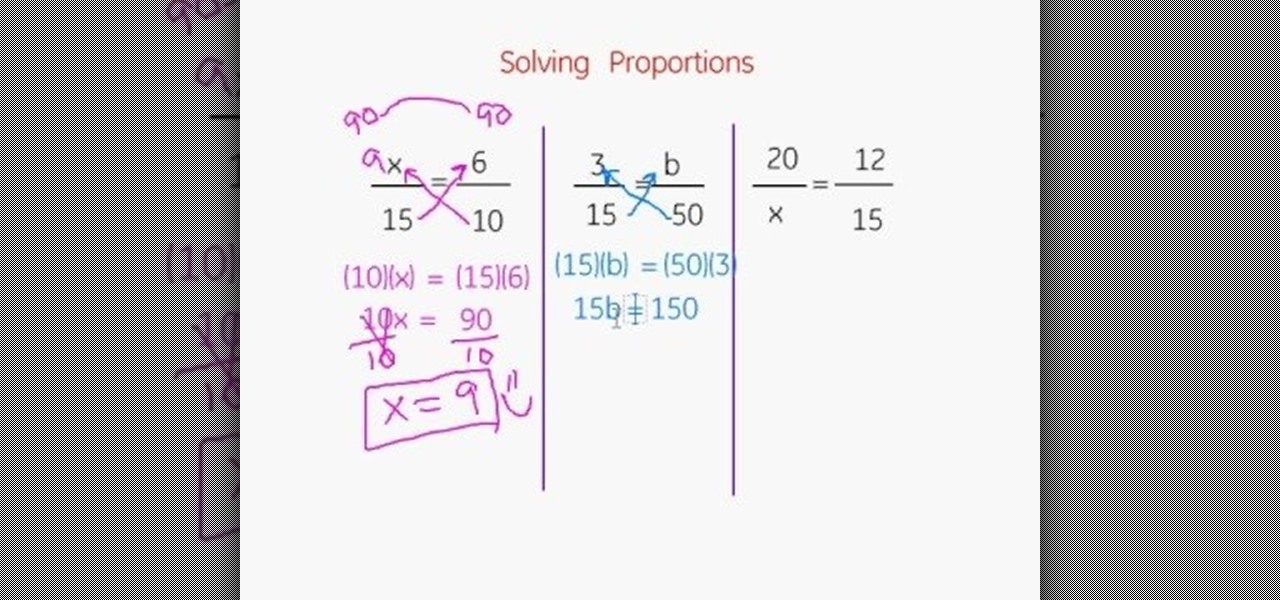
How To: Solve proportions
This video describes about how to solve multiple proportions. The first step describes how to cross multiply and solve the equation. There are three proportions solved in this video and they are explained how to arrive the final answer. The first step is multiplying the denominator with the opposite numerator and an answer is arrived and again the same is multiplied to arrive a final answer. Two more proportions are solved in the same manner. The video camera is focused on the white board in ...

How To: Derive the area of a circle
This video is about deriving the area of a circle of radius 'r' using polar co-ordinate. First, we draw a circle and its radius 'r'. Then draw another radius close to it, so that it forms a small triangle-like figure. To find the area of the complete circle, divide the circle into similar small triangles. The area of each triangle is given by half the product of its perpendicular and the base. We give the angle between the two radii as d?. We get the area of the small triangle by substituting...

How To: Multiply 2 digit numbers using the grid method
This video shows the method to multiply two digit numbers using the grid method. First make a grid of three rows and three columns. Put a cross in the first row and first column or the (1,1) position. Separate the ones and the tens in the number. In our example 43 is broken into 40,3 and 56 is broken into 50,6. Put these numbers in the remaining places in the first row and first column. Now multiply every number with the other and place it in the corresponding location in the grid. In our exa...
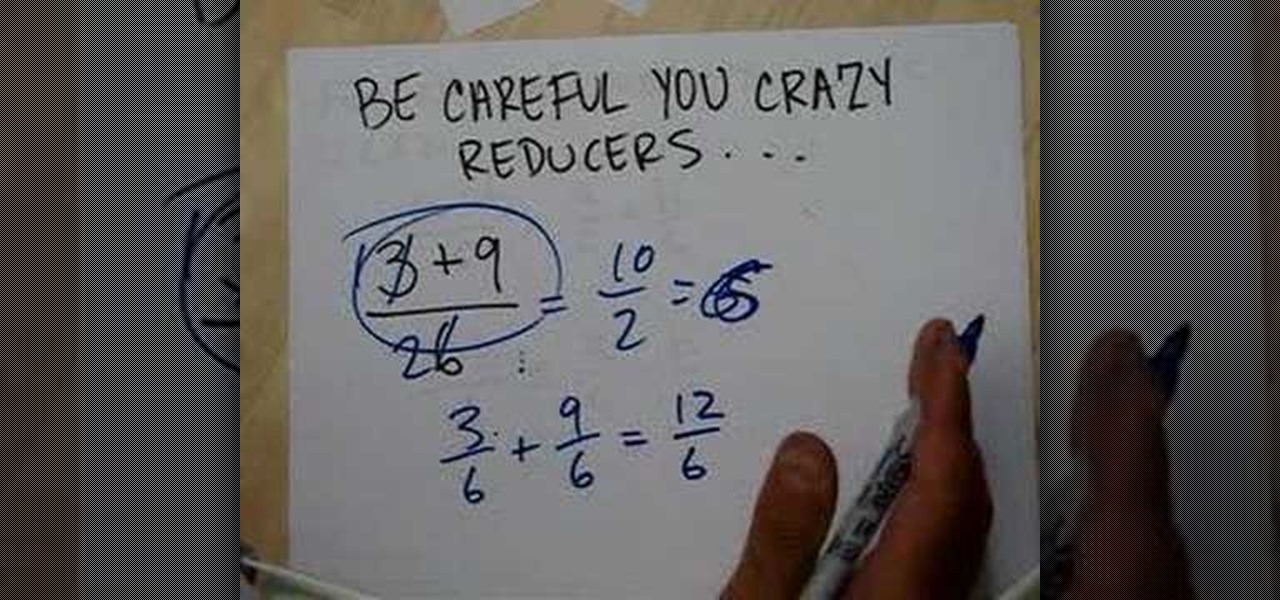
How To: Divide real numbers
This video illustrates the method of dividing real numbers. The process is composed of the following steps -Step 1Take any two real numbers. Convert them to rational numbers taking denominator as one.Step 2Find the LCM of their denominators and multiply both the numerators and denominators by the LCM.Step 3Now find the reciprocal of the second number and move to the next step.Step 4Now divide the numerators obtained. The denominator are also to be divided and the quotient obtained should be r...

How To: Define an indefinite integral in calculus
In this video tutorial, viewers learn how to define an indefinite integral in calculus. Finding the anti-derivatives of a function is called anti-differentiation. The f(x) is the derivative of F(x), while F(x) is the anti-derivative of f(x). If F(x) is the anti-derivative of f(x), then F(x) + c are all anti-derivatives of f(x). This video is very descriptive and clearly explains all the functions of this mathematical function. This video will benefit those viewers who are students, and are in...

How To: Solve percent proportions
A percent problem is one in which you are given a quantity and asked to compute the value of a percent of it. You may also be given the whole quantity and a part of it and asked to compute the percentage of the part in the whole. To do these kind of problems you need to use the rule which states that the ratio of the part to the base it equal to the ratio of the percent to hundred. That is part/base = percent/100. This comes from the definition of percentage which states that percentage is eq...

How To: Solve word problems using proportions
This video shows the method to solve word problems using proportions. In the given problem, we have to find the time taken by a person to type 390 words if the person takes 1 minute to type 30 words. This can be solved using proportions. We take two fractions which are equal. We type '30 words' in the numerator of the first fraction and 1 minute in its denominator. This fraction must be proportional to the second fraction. The second fraction has '390 words' in the numerator and the variable ...
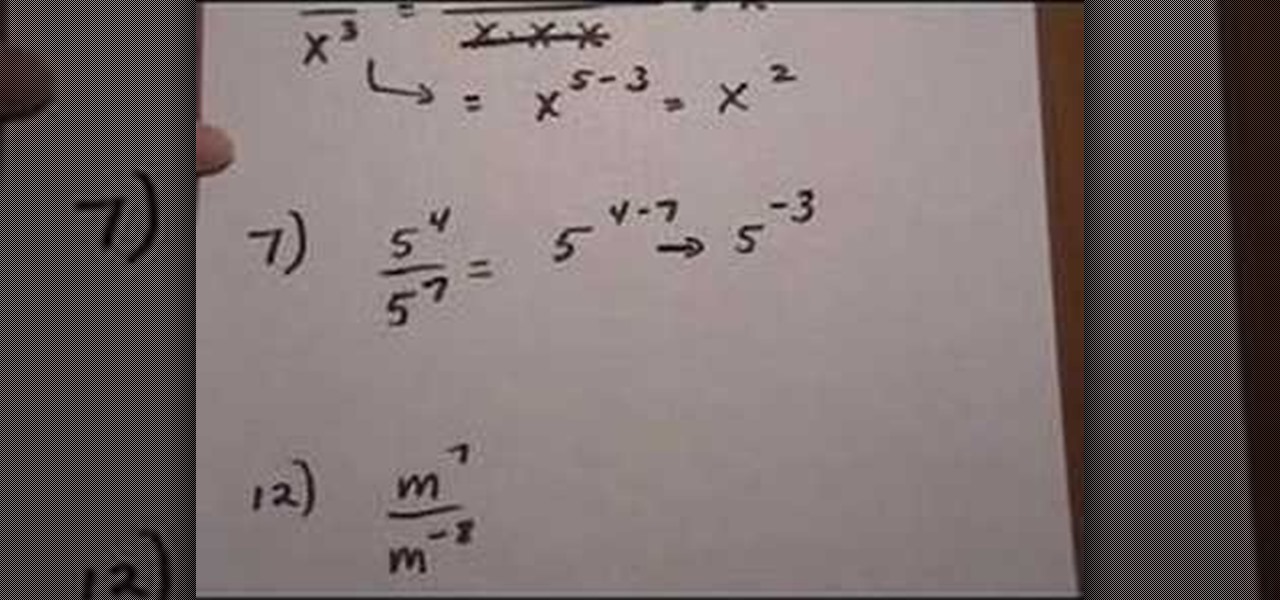
How To: Simplify exponential expressions via the quotient rule
This video demonstrates the quotient rule as applied to exponential expressions that appear in the form of, to use the word loosely, a fraction. The name, "quotient rule", refers to the fact that it applies to expressions which are divided by other expressions. The video begins by explaining that the quotient rule allows expressions in this form to be simplified if they contain like bases (i.e., the terms are of the same variable). The quotient rule allows the expression to be simplified by s...
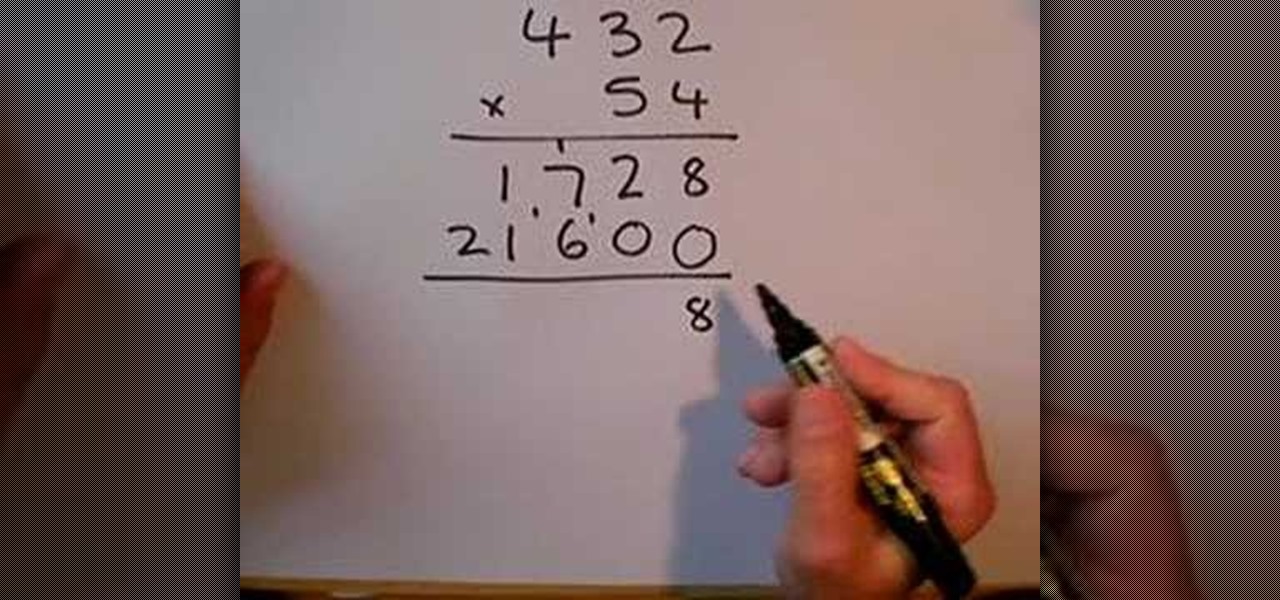
How To: Do long multiplication
In this video the instructor gives you sample as of how to SLEP long multiplication. You start by breaking the numbers up to simpler forms. If you have a two digit number that your multiplying by a another two digit number you multiply the first two digit number and then buy the second digit of the second two digit number. You have to remember to carry the remainders. You then add your two multiplicative lines together giving you the sum. this can be done to cover any set of multi-digit numbe...

How To: Factor out when doing rational expressions in algebra
This video shows the method to simplify rational expressions. The example used in the video is multiple of 4 and x square plus multiple of 4 and x plus 1 or (4x^2 + 4x + 1)/(2x^3 + 11x^2 + 5x). As the first and last term is a perfect square we get the simplified numerator as (2x + 1)(2x + 1). Next, the denominator is simplified. Taking the common factor out we get x(2x^2 + 11x + 5). Now we factorize 2x^2 + 11x + 5. We get (2x + 1)(x + 5 ). Now, writing the terms in numerator and denominator w...

How To: Use differential equations to solve for velocity
The guy first gives the definition of differential equations. He explains that a differential equation is an equation that contains the derivatives of an unknown function. He then gives some examples of differential equation and explains what the equation's order means. After that he gives an example on how to solve a simple equation. He calculates it and gives examples of graphs. Then he explains what a general solution is and how to narrow down the number of solutions using data from the pr...

How To: Build a giant geoboard with your kids
Geoboards are fun tools to teach your child the basic concepts of shapes and how they work in math; any kid would love a gigantic one! Firstly, you need to obtain a pegboard (what they hang merchandise on in hardware and similar stores). They usually come in 4x8' sheets, so you may need to ask an employee to cut one into fourths for you. The fourth piece should have 64 holes in 8 rows of 8, which means you need 64 nuts and bolts to make the board. Assembly is a no-brainer; you and your kids s...

How To: Reduce a fraction to its simplest form in basic math
Fractions are numbers of the form a/b, where a and b are integers. Fractions are also called as ratios. Fractions are further divided into proper fractions and improper fractions. Proper fractions are those where the numerator is less than the denominator and improper fractions are those where the numerator is greater than the denominator. As fractions are ratios a fraction can have many equivalent forms. Multiplying the numerator and denominator of a fraction with a same number gives a fract...