In this video the author explains how to identify the less than (<) and greater than (>) symbols and when to use them. She explains to us to relate the numbers to animals stating that the smaller numbers are smaller animals and bigger numbers are bigger animals. Now she tells us to imagine that smaller animals are eaten up by the larger animals. So she shows a smaller number comes on the left side of '<' sign and bigger number comes on the right side of '<' sign stating that the bigger number looks like its going to eat the smaller number. Similarly she explains about the '>' sign. Now she demonstrates this with a couple of examples. This video clearly explains how to learn the symbols of < and > using intuitive methods.
Just updated your iPhone? You'll find new emoji, enhanced security, podcast transcripts, Apple Cash virtual numbers, and other useful features. There are even new additions hidden within Safari. Find out what's new and changed on your iPhone with the iOS 17.4 update.









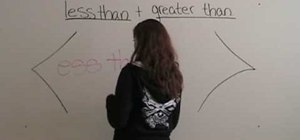










1 Comment
Thanks for the post
Share Your Thoughts