Active Math Posts

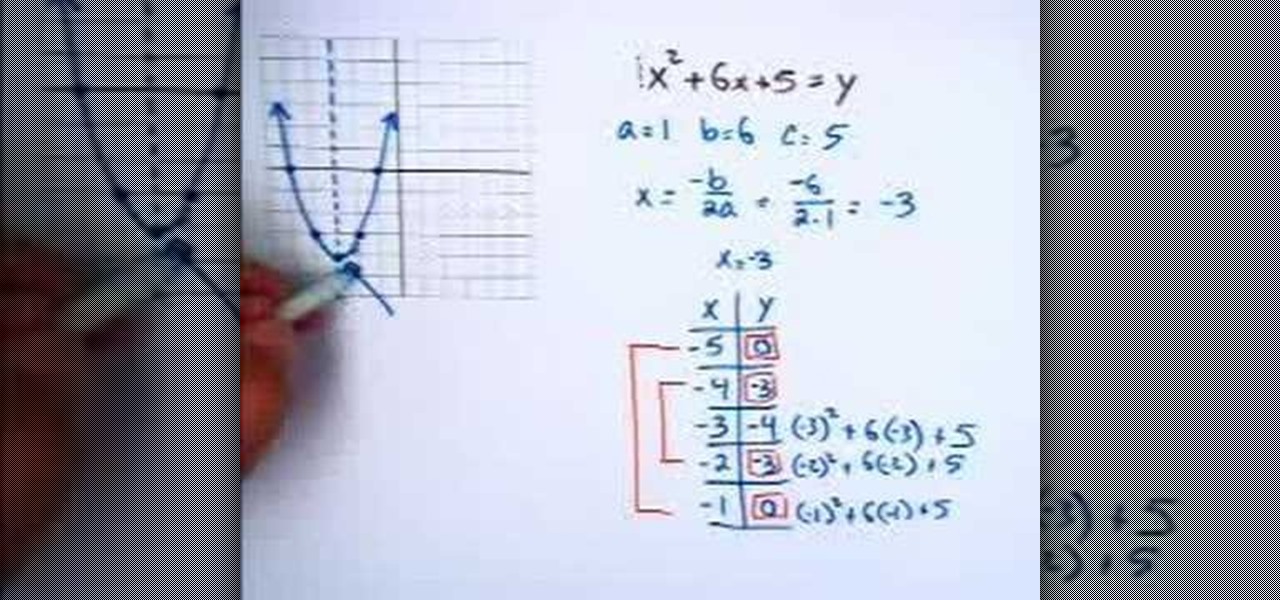
How To: Graph quadratic equations
In this video, the instructor shows you how to graph quadratic equations. When you have a quadratic equation in terms of x and y, first try to identify the coefficients of the terms. Now use front end of the quadratic formula to find the line of symmetry which is the first half of the vertex using the formula x = -b/2a. This gives the line of symmetry. Next, plot the line using a few points starting at the line of symmetry. Take sample values of x and find the corresponding values of y on eit...

How To: Determine the age of a fossil using carbon-14
If you have a fossil, you can tell how old it is by the carbon 14 dating method. This is a formula which helps you to date a fossil by its carbon. If a fossil contains 60% of its original carbon, how old is the fossil? The half life of carbon 14 is 5600 years. That means this is how long it takes for half the nuclei to decay. After 5600 years, if we start with a gram, we end up with half a gram. This rather complex formula shows you how to solve this puzzle using accepted scientific methods.

How To: Use math reflections in pre-Algebra
The tutorial is part of a full lesson of pre algebra. This video teaches you what reflection is as a mathematical term. In the beginning of the video, the video maker draws 4 shapes labeled MNOPQ, ABCDE, FGHIJ and RSTUV. The first question in the video asks to "Name the figure that represents a reflection of ABCDE over the X-axis." The woman in the video repeats the question, stating the horizontal line is the X-axis and asks for the reflection image. She puts her hand on ABCDE and flips her ...

How To: Understand mean and standard deviation
Keith M. Bower explains the meaning of mean and standard deviation. This educational video gives insight in the basics of statistics. The relations between population mean and sample mean and between population standard deviation and sample standard deviation are explained. The mean gives an idea on the central tendency. Standard deviation gives an idea about how spread out the data are. Keith also explains how these two parameters, the joint sufficient statistics, define a normal distributio...
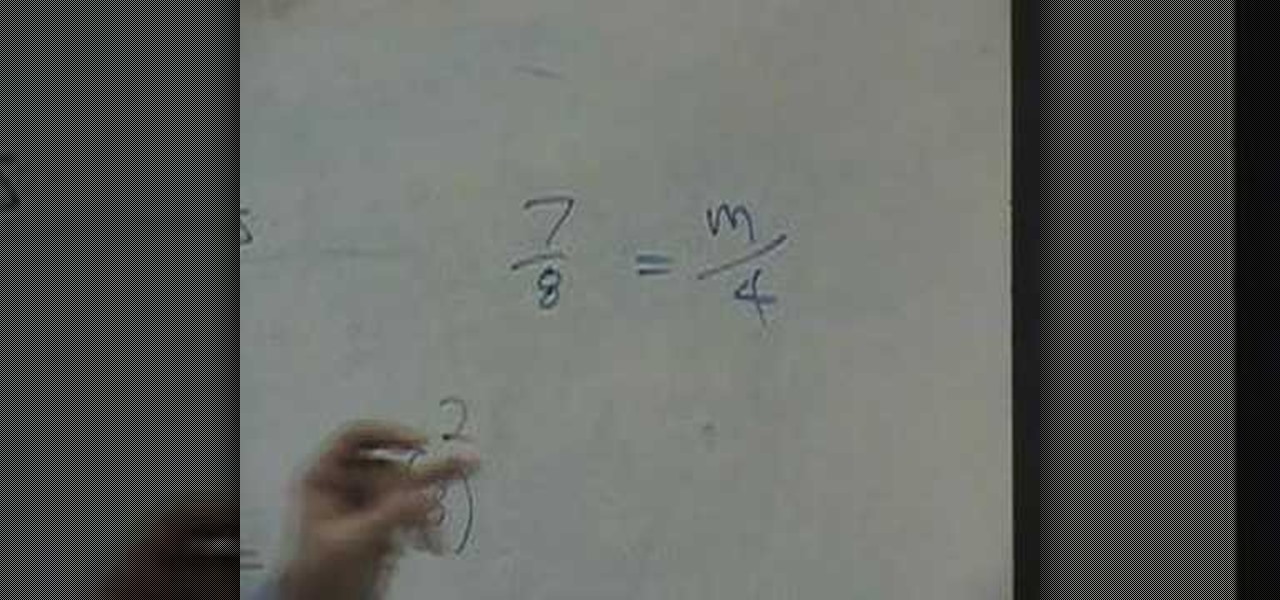
How To: Solve word problems with proportions
In this video the instructor shows how to use proportions to solve fractions. When you have a proportions problem with an unknown term, cross multiply and divide it to get the value of that unknown term. For example if given 7/8 = m/4, cross multiply 7/8 with 4, giving 7/2 which is the value of the unknown variable m. So if two quantities are proportionate then you can equate them as shown in the video and cross multiply to get the value of any unknown variable. Proportions are just fractions...

How To: Simplify expressions with different exponents
This video shows the method to simplify expressions with different exponents. The video starts with the explanation of 16 raised to the power 1/4. This can be solved by taking the nth or the 4th root of 16 where n stands for the denominator of the fraction. Then the video explains 8 raised to power 4/3. This can be solved in two ways. First one involves taking the cube root of 8 and raising it to the power of 4. The second method involves converting 8 into 2 raised to the power 3 and taking t...

How To: Understand deductive reasoning
In this video, Robert Ahdoot becomes "surfer dude" and shows us the ways of deductive reasoning, as relating to geometry. He begins with a simple example of a syllogism, taking two premises and using them to form a conclusion. This is called the Law of Syllogism. This concept is then used for geometric statements. If two angles are complementary, they sum to 90 degrees. If two angles sum to 90 degrees, then they are acute. By the law taught, it can be said that if two angles are complementary...

How To: Use simulations in pre-Algebra
This is a video from yourteacher.com on simulations for Pre Algebra. It explains what simulations are and gives an example problem. The teacher reminds us that it is important to remember that there can be more than one simulation for a problem. The teacher suggests a simulation for the problem given and suggests how many times to run the simulation. The teacher makes a simulation for what sex a child is by flipping a coin and suggests to flip the coin 50 or 100 times. The teacher also explai...

How To: Find the point slope form of a line equation
This is a mathematical instructional video on finding the point slope form of a line equation. This technique allows you to find the x and y intercepts of a line. The point slope form is (y-y1)=m(x-x1). The instructor tells you what each of the variables represents, and shows an example. He then shows you how to find the slope-intercept form from the point slope form. Finally, he shows you how to graph the line using both of the equations. He shows you how to find the equations with different...
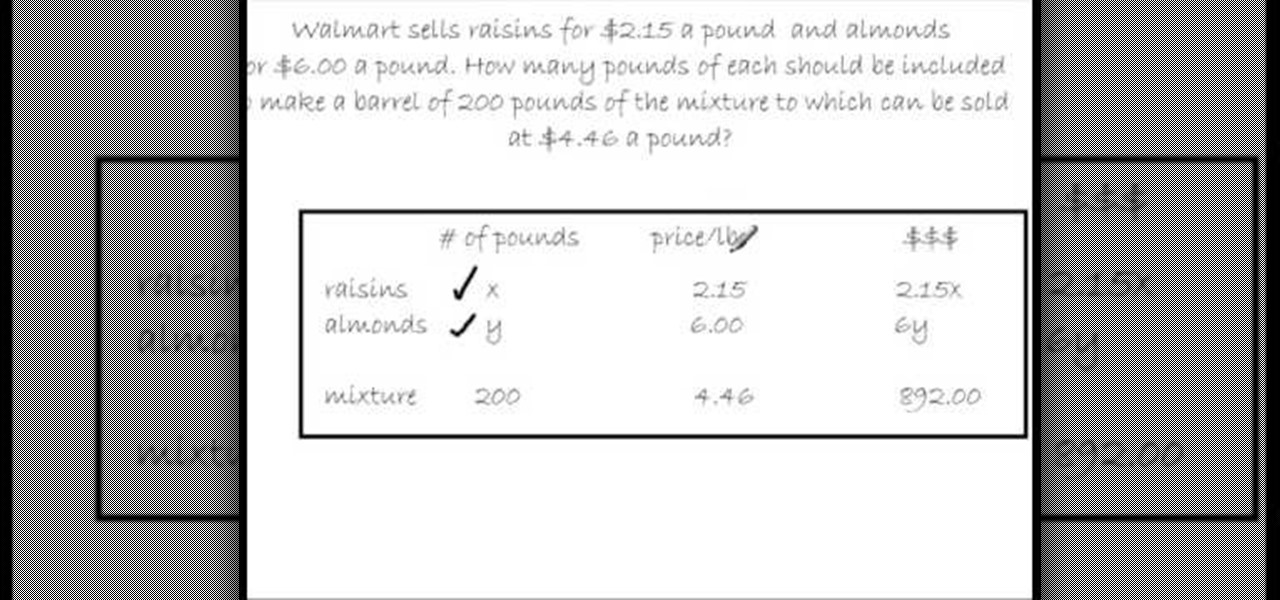
How To: Algebraically solve mixed quantities problems
In this video the instructor shows how to solve mixture problems using two variables. Usually in these kind of questions the problem statement goes like, if A costs $x for a pound and B costs $y for a pound, in what ratio should they be mixed such that one pound of the new mixture sells for $z a pound. So, in these kind of problems start with a box where you list down all the given data in the form of a table as shown in the video. Now denote the unknown quantity of A and B by two variables a...
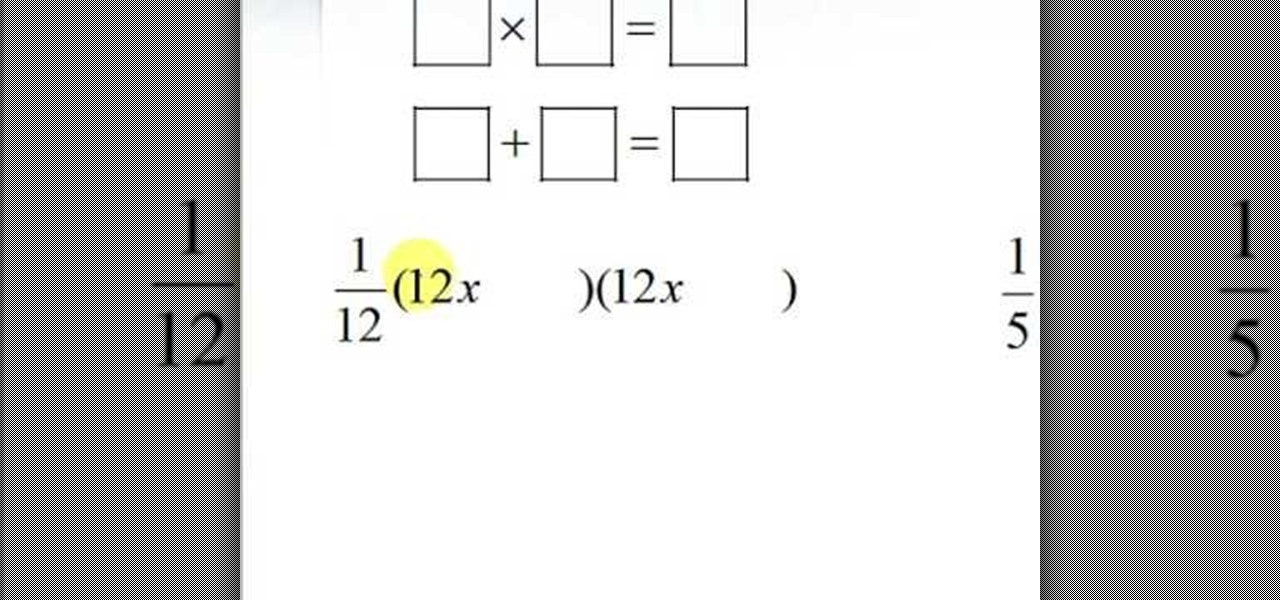
How To: Factor trinomials in a very simple way
In this video, they demonstrate how to factor a trinomial. A trinomial is a polynomial with a quadratic term in the form, ax^2+bx+c. To factor this polynomial first multiply the a and c term. You must fine two numbers that multiply to a*c and add up to b. Once you have figured out the two numbers you place the two numbers (D and E for example) in the equation (1/a)(ax+D)(ax+E). It takes a bit of practice to be good at deciding what D and E are, but the best way is to make sure that D*E = a*c ...
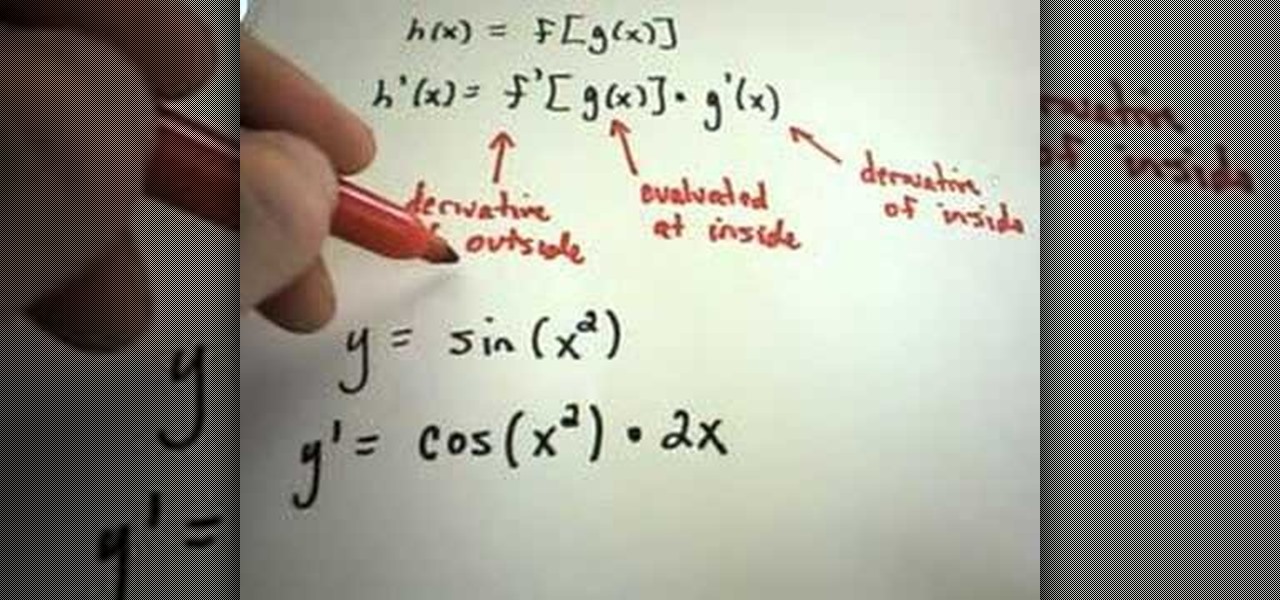
How To: Use the Chain Rule for finding derivatives
JustMathTutoring This video shows the procedure of finding derivatives using the Chain Rule. The Chain Rule states that the derivative of a composition of functions is the derivative of the outside function evaluated at the inside multiplied by the derivative of the inside. This can be stated as if h(x) = f[g(x)] then h'(x)=f'[g(x)]g'(x). This is explained by two examples. In the first example we find the derivative of the sine of square of 'x'. We take the derivative of sine at square of 'x'...

How To: Simplify complex fraction w/ 3 fractions top & bottom
You Tube User robichaudd teaches you how to simplify a complex fraction with 3 fractions top and bottom. Your result should be 1 fraction over 1 fraction. To do this you must find the L.C.D. at the top, which x cubed. That is the largest variable there. Thus, the L.C.D. at the bottom is x squared. Now you want to make each x below the fraction line be x cubed, respectively x squared. You then have one large fraction over one large fraction. But that is just one large fraction multiplied by th...
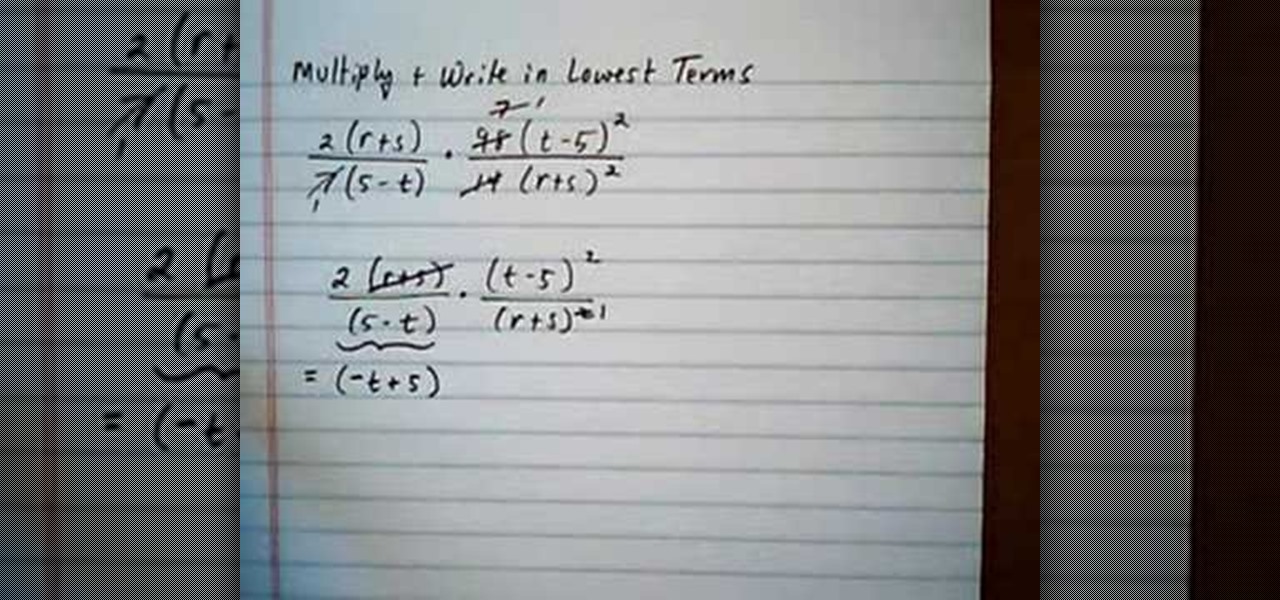
How To: Multiply rational expressions with opposite signs
In this video the instructor shows how to multiply and write rational expressions in lowest terms. The fist thing you need to do is cancel out the common factors in the numerator and the denominator. You can cancel a term in the top with a term in the bottom even if they are diagonal as long as one is in numerator and the other is in the denominator. After cancellation if you have a term in numerator and an identical term in the denominator but with opposite signs, then pull out the negative ...
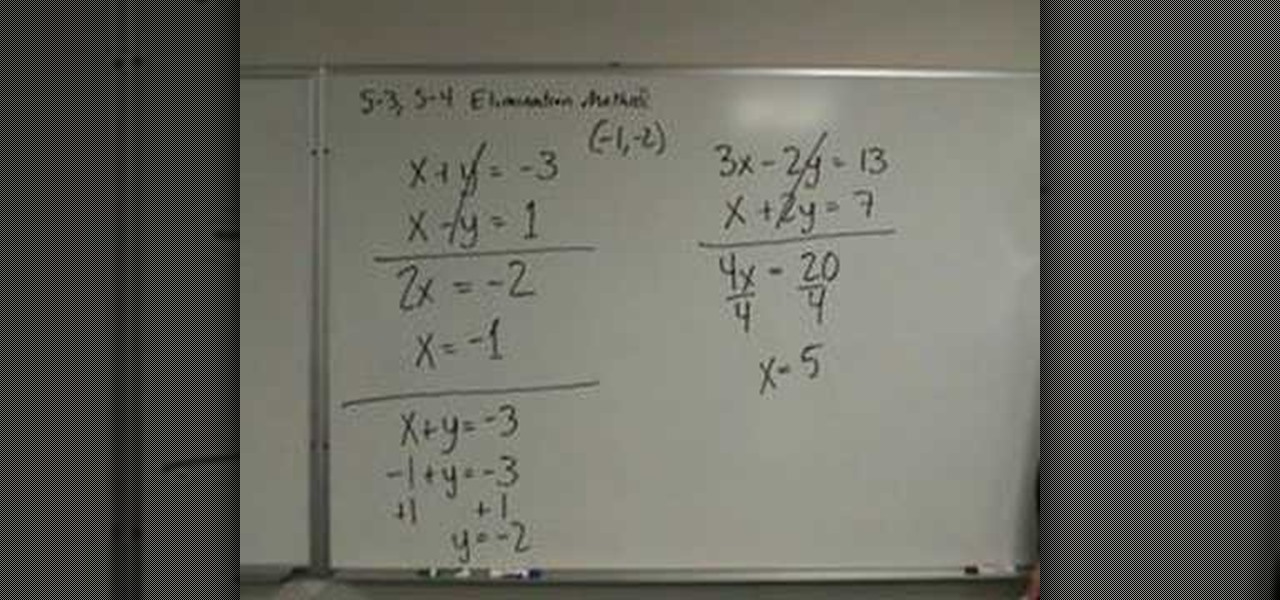
How To: Solve a system of equations w/ the elimination method
The video shows us how to solve a system of equations with the elimination method. First write the two equations one on top of the other, as it is going to be elimination method and it is recommended to write it in that way. Here the 2 equations are x+y=-3 and x-y=1. In the elimination method we need to add the 2 equations by columns. So adding it column wise we get to have 2x=-2 and solving this we will get the value of x=-1. Then you need to substitute this value of x in any of the two equa...

How To: Graph x squared & the square root of x
In this video the instructor shows how to sketch the graph of x squared and square root of x. The first equation is the x squared which is y = x * x. Now to sketch this take a sample values of x and substitute in the equation to get the value of y. Similarly find the set of points for the equation. Finally plot these points and sketch this graph which is in the form of a parabola. The curve is in the form of alphabet 'U' with its vertex at the bottom. Now similarly take the square root of x e...
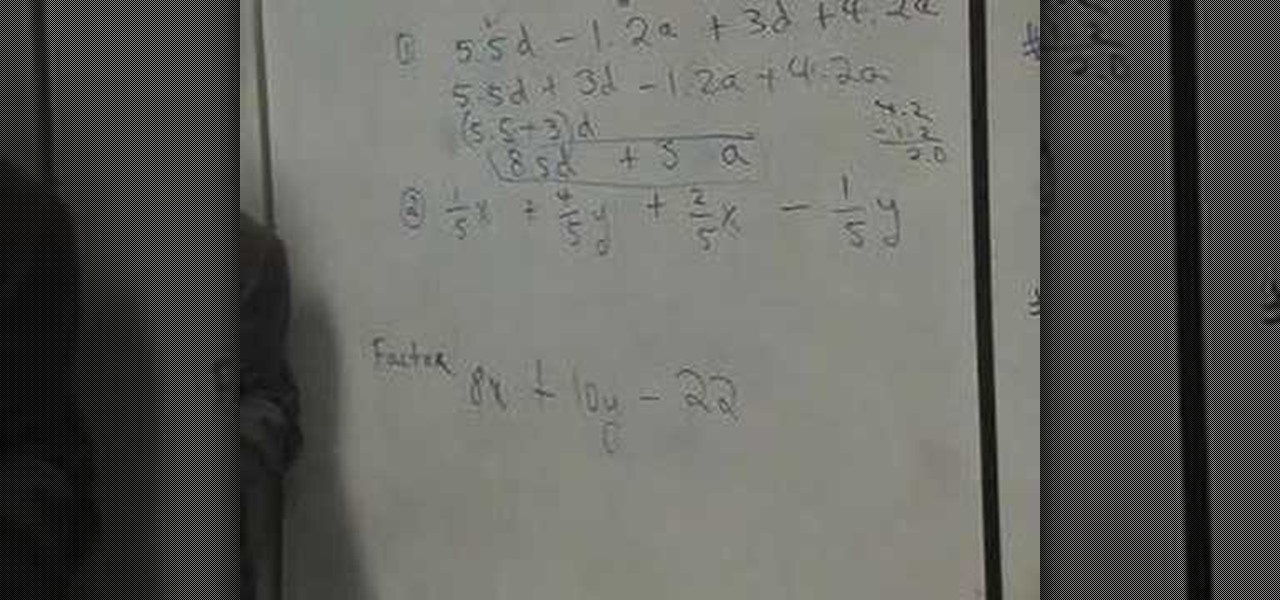
How To: Factor and collect like terms
In this video, the instructor shows how to collect like terms and factorize. When you are given a linear equation, the first thing you do is to try to organize it. Pair up the like terms. Add the numerical coefficients of terms with the same variables. This is called collecting the like terms. In case you see any common factor across all the terms, pull it out and tag it to the parenthesis. In this way, you can factorize the equation. Next, bunch together your like terms and sum them up. The ...

How To: Derive the area of triangle using trigonometry
This video teaches the method to find the area of triangle using law of cosines and law of sines together with the area formula. Law of cosines is used when you have the length of three sides. It states that the square of side 'a' is equal to addition of the squares of sides 'b' and 'c' minus the product of 2, b, c and cosA. The values of sides are substituted and angle A is found. This is substituted in the area formula which states that the area of a triangle is equal to the half of the pro...

How To: Find the area of a right triangle using simple math
It is easy to find out that right triangle is only half of the square. And again there is a rectangle with a triangle shaded in red color. The red triangle is half the area of the rectangle. But to calculate just the area of triangle, we can calculate the area of the rectangle whose area is length times width. When we have a rectangle with its length and width as 4u and 2u respectively then the area of that rectangle will be equal to 8u(squared). But we already know that the triangle is half ...
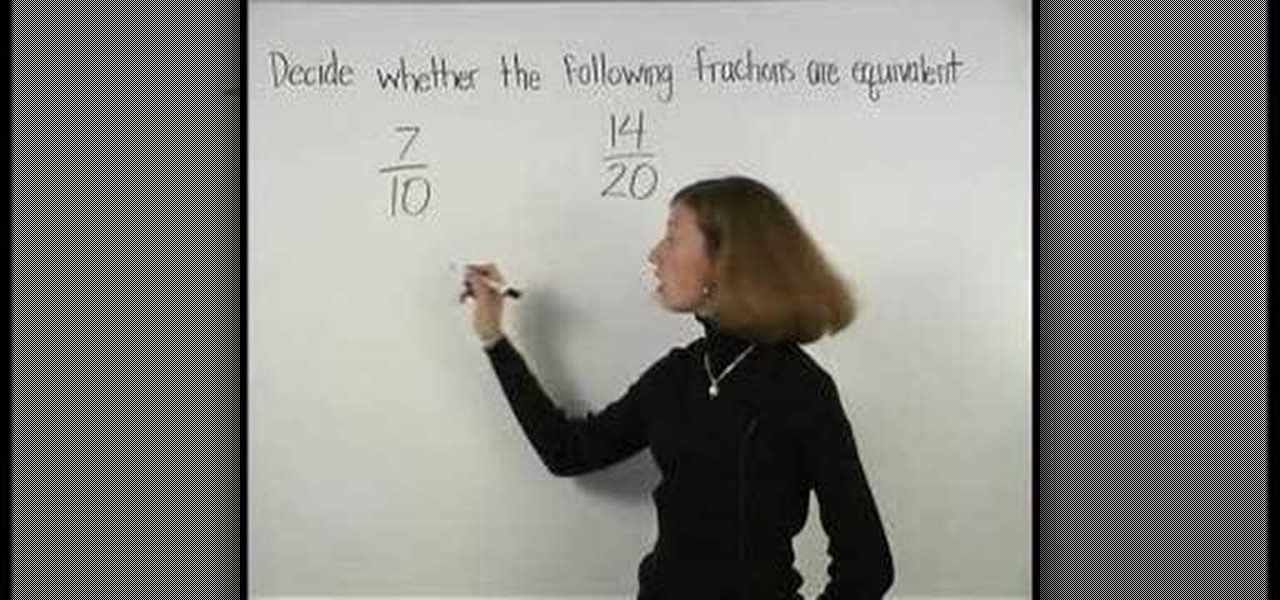
How To: Understand equivalent fractions
In this video the instructor teaches about equivalent fractions. When given a problem to determine if two fractions are equivalent fractions the first thing to do is write them in the lowest terms. A fraction is said to be in the lowest terms if the greatest common divisor of both numerator and denominator is one. So cancel the common factors in the numerator and the denominator till you arrive at the lowest form and finally compare them to determine if they are equivalent. An equivalent frac...

How To: Calculate variance in a set of data
The video is about how to find the variance of the set of data. They found the variance by using the variance formula. Variance formula was represented by square of S, whereas S is the Standard Deviation.

How To: Write a sum/difference of logarithms as a logarithm
To write the sum or difference of logarithms as a single logarithm, you will need to learn a few rules. The rules are ln AB = ln A + ln B. This is the addition rule. The multiplication rule of logarithm states that ln A/b = ln A - ln B. The third rule of logarithms that deals with exponents states that ln (M power r) = r * ln M. Using these three rules you can simplify any expression that involves logarithms to arrive at a single logarithm. The instructor shows how to apply these rules to a f...
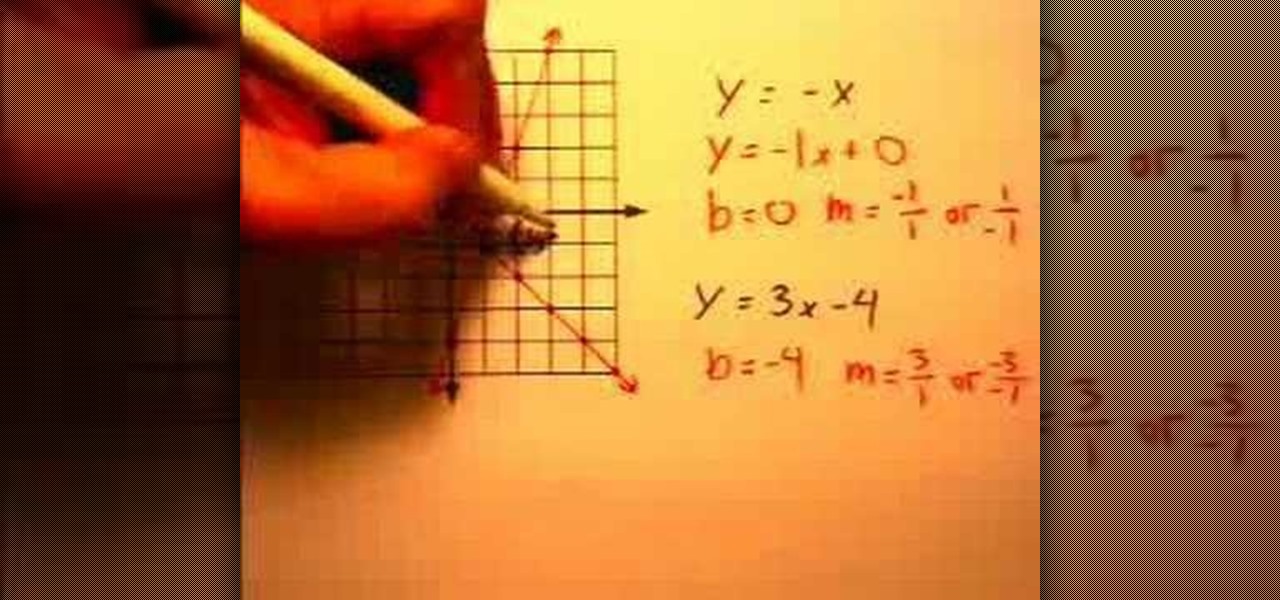
How To: Solve systems of linear equations by graphing
In this video the instructor shows how to solve systems of linear equation by graphing. A system of linear equation is equations of two lines that are to be graphed on the same coordinate axes. Now take the first equation and write it to form y = mx + b. Now extract the value of slope m and graph the line as shown in the video. Similarly graph the equation of the second line as shown in the video. Now if the two lines intersect at a point, that point is the solution to the system of that line...
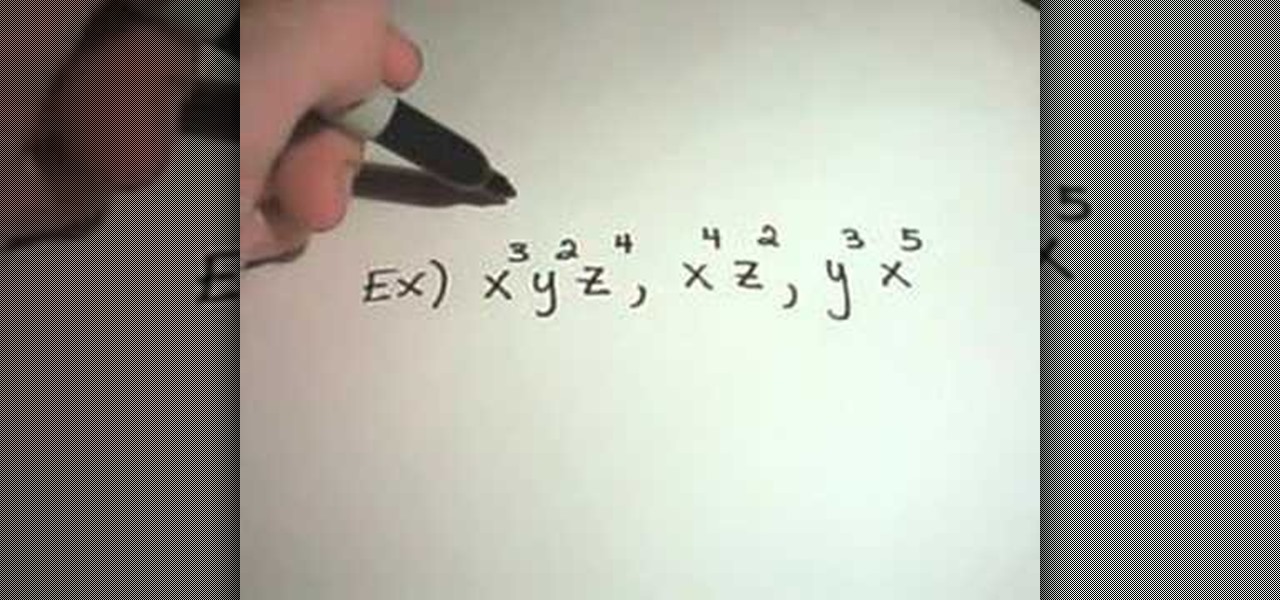
How To: Find the greatest common factor, GCF
In this tutorial the instructor shows how to calculate the greatest common factor, or GCF. While computing greatest common factor, you are pulling out the smallest exponents of any common factors along with the factor. Finding the greatest common factor is similar to finding the least common multiple. When given any numbers to find the greatest common factor, the first step in the general procedure to be followed is to break each number down into its factors. You need to break down the number...

How To: Evaluate functions on a calculator TI-89
In this how-to video the person gives a detailed evaluation of the functions of the ti-89 calculator. The video is a short but informative look at the Ti-89 calculator. During the video the person shows a difficult math problem and shows how to use the Ti-89 calculator to solve that problem. The video uses some of the functions on the calculator and shows a display of where the buttons are located on the calculator. It also shows how to properly use the calculator to solve the problem while w...
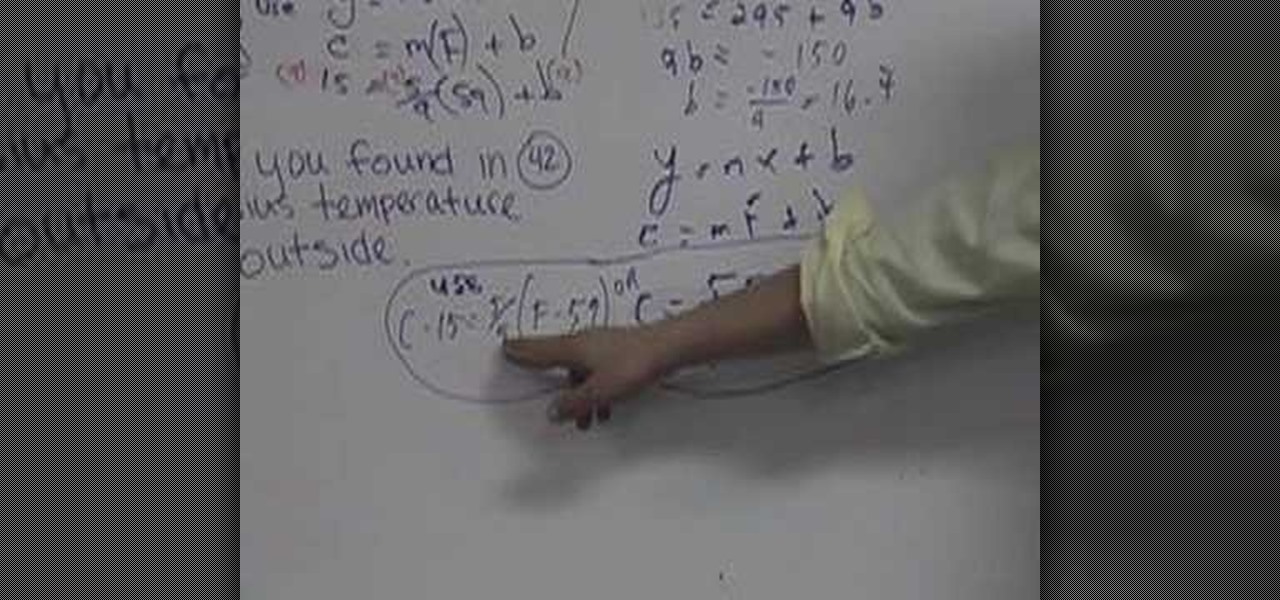
How To: Convert temperature using y = mx + b
In this video the instructor shows how to do temperature conversions using y = m*x + b. Now if Celsius is represented by the variable C and Fahrenheit is represented by the symbol F, you can replace then in the previous equation in place of the variables x and y giving you the equation C = m*F + b. Now to solve for the values of the constants m and b you need to have values of two sample temperatures in both Celsius and Fahrenheit. Take the first sample and substitute in the above equation gi...

How To: Solve radical equations in algebra
The video demonstrates the solving of radical equations in algebra. The first thing to be done is to keep the radical number on one side and the other numbers on the other side. The radical is then changed to a rational number by squaring, cubing etc. Once the roots are removed, it becomes a simple equation which can be solved by keeping the unknown number on one side and the rest of the numbers on the other side. The value, thus arrived at, is checked by putting the value of the unknown numb...
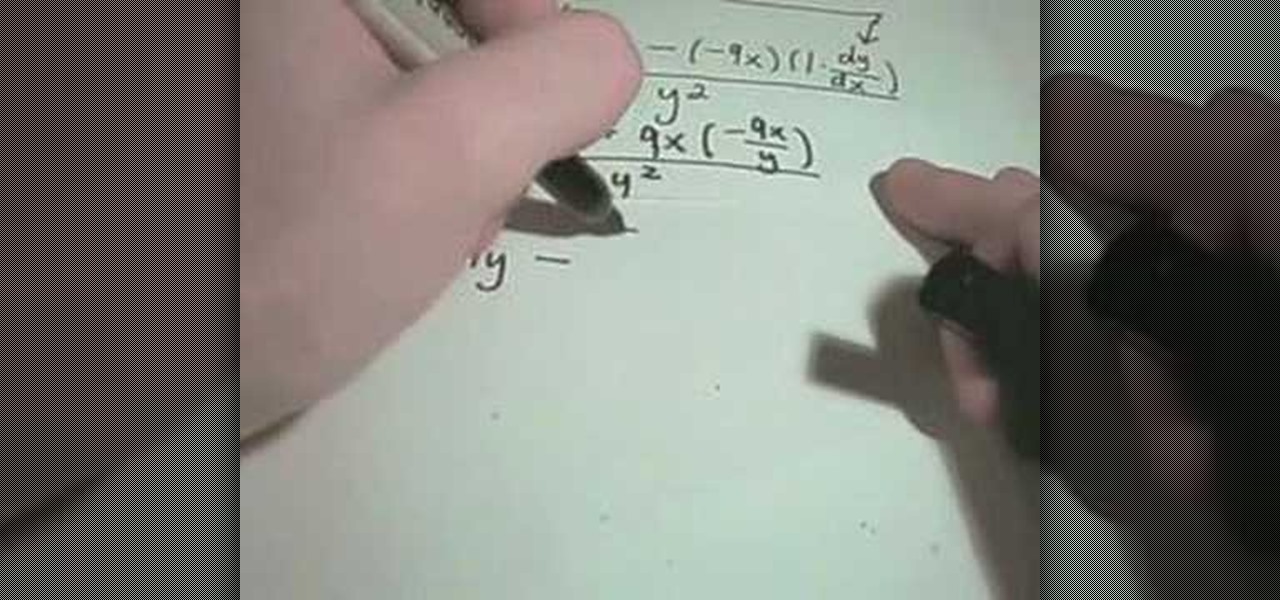
How To: Use implicit differentiation
Taking this formula 9x²+y²=9 your instructor shows you how to find the solution for the variable y. Finding a second derivative is no more difficult that finding the first derivative, you only have to do the problem equation through twice. The derivative of 9x² will be 18, of y² will be 2y [this is the same as 2(y), 2 x y or 2 * y]. The problem now goes -18x + 2y dy/dx=0. This equation is solved for dy/dx making the next step in the problem go -18x 18x+2y dy/dx=0-18x, 2y dy/dx= -18x. The next...
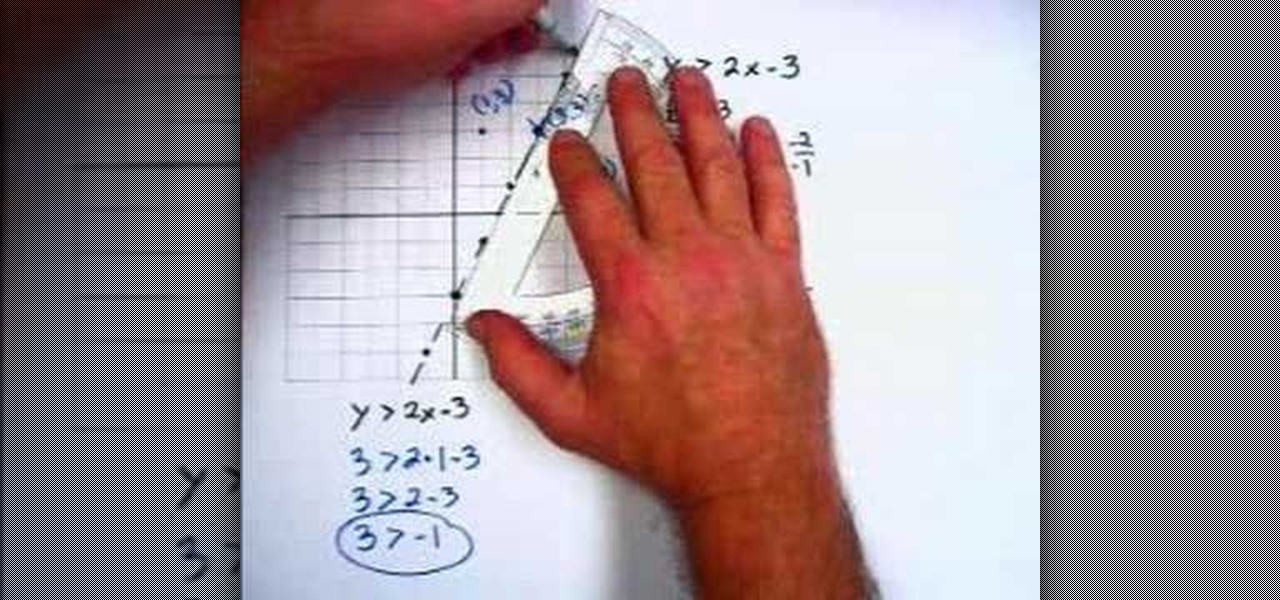
How To: Graph linear inequalities
In this video the instructor shows how to graph linear inequalities. A linear in a equation is almost similar to a linear equation except for the sign in the equation. Now treat the in equation as a linear equation and graph the line. So substitute the lesser than or greater than symbol in the liner in equation with the equals to sign and graph the equation. Find the slope of the equation and identify the points that the line passes through. Now take a point on the either side of the pointed ...

How To: Solve percent equations
In this tutorial the instructor shows how to solve percent equations. The general form of a percent equations is that a is b% of c. As there can be three kinds of variables a, b, c, the questions involving percent equations can be of three types having one of the three variables unknown. These kind of percent statements can be solved easily by setting up an equation. So, to convert percent statement into a equation replace the unknown term with n, the 'is' term with equals sign and the '%' si...
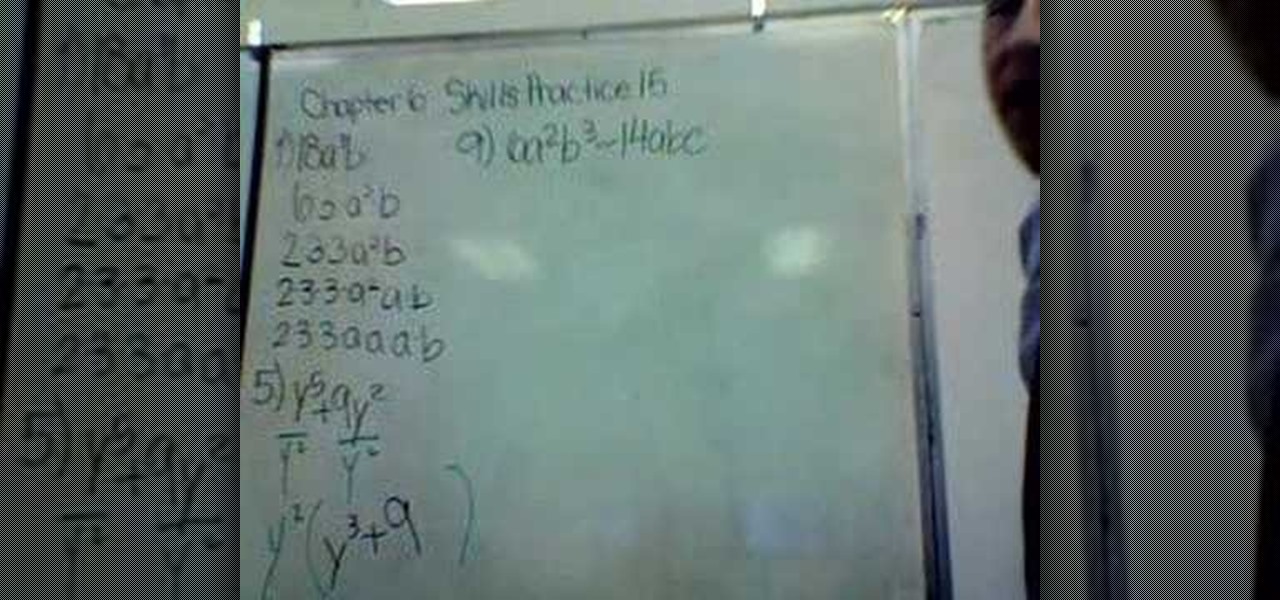
How To: Factor the GCF and difference of squares
In this video the instructor shows how to factor the GCF and difference of squares. When you are asked to factorize a number or monomial or a polynomial, the way to do is break it down into individual terms. When asked to factorize a binomial, try to pull out any common terms and factorize the simplified equation. When you are asked to factorize the difference of squares use the general formula which states that the factors of (a*a - b*b) is (a-b) * (a+b). Now substitute the given values in t...

How To: Use the distance formula
YAYMATH. This video is a demonstration of usage of the distance formula to find the distance between two given (x,y) points. In this video, the tutor guy who is teaching the distance formula to his students takes an example of two (x,y) points such as (5,-1) and (11,7). He then writes the distance formula on the board. The formula goes like this, the distance between two points, denoted by 'd' is equal to the square root of the sum of the square of (x2-x1) and the square of (y2-y1) where (5,-...

How To: Understand why you cannot divide by zero
This video discusses the number zero in division. When dividing numbers, there are ways to check your math, like multiplying the two numbers. When you multiply zero with any other number, it still is zero. The video goes on to discuss indeterminate answers. If you were to divide a zero by a zero, your calculator would come up with an error message. But there are real results to these odd equations and they are indeterminate. The indeterminate doesn’t really show up in everyday living, but in ...

How To: Solve rational equations
In this video the instructor shows how to solve rational equations. If you have fractions in your equation, then you need to factorize the denominators first. Now compute the least common denominator of all the denominators of the fraction. Next multiply both sides of the equation with the least common denominator. This cancels out all the denominators of all the fractions and you are left with a linear equation. Now simply multiply the remaining terms in the numerator and add common terms to...

How To: Find circumference and area of a circle
In this video tutorial, viewers learn how to solve for the circumference and area of a circle. The circumference is the distance around a closed curve. The formula for circumference is C= pi x d. The diameter is two times the radius (d= 2r or r= d/2). The value of pi is approximately 3.14. The formula for the area of a circle is A= Pi x r^2. This video provides examples and demonstrations on how to use and solve with both the formulas. This video will benefit those viewers who are struggling ...

How To: Use line segments in pre-Algebra
This video shows the way to name a line segment. A line segment begins and ends with an end point. We can name a line segment by naming the two end points of the line segment. The example shown in the video shows a line segment that ends with points named 'A' and 'C'. So, we can name this line segment as segment 'AC'. This can also be named as segment 'CA'. The example shown consists of a point 'B' in between 'A' or 'B'. We cannot name the line segment as segment 'AB' or 'BA' and segment 'BC'...

How To: Graph square root functions & inequalities
On Yay Math, Robert Ahdoot, founder of Yay Math, will show you some square root functions and some inequalities. He begins with the problem y=x². Then he makes a sketch with two intersecting lines in a t shape. The problem is illustrated by a curved U shape, the U's bottom resting on the horizontal bar, which represents x, while the center takes the vertical line. The vertical bar represents y. This U is directed up because the x² is a positive number. If the number were negative, the U would...
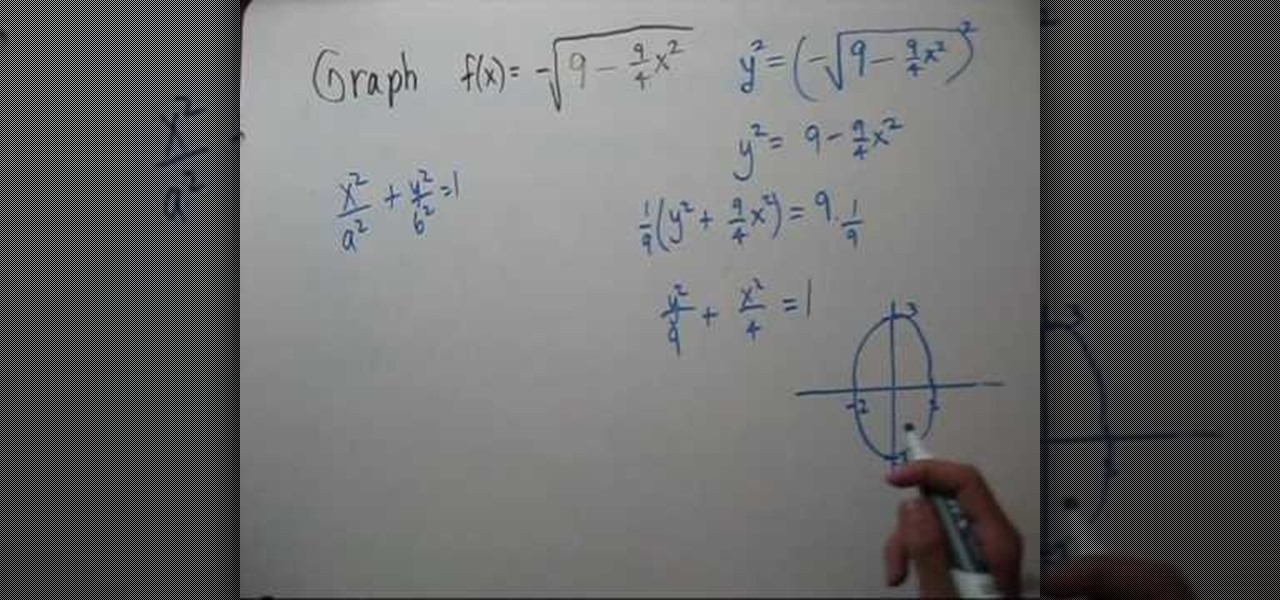
How To: Graph half an ellipse
If you are given an equation of ellipse in the form of a function whose value is a square root, you may need to simplify it to make it look like the equation of an ellipse. Now equate the function to a variable y and perform squaring on both sides to remove the radical. Now simplify the equation and get it in the form of (x*x)/(a*a) + (y*y)/(b*b) = 1 which is the general form of an ellipse. Now you will have the x and y intercepts which are a and b respectively. Using this values graph the eq...

How To: Change Fahrenheit to Celsius
This video is a tutorial on how to convert Celsius to Fahrenheit. The title of the film says it will teach you how to convert Fahrenheit to Celsius, but it does not. It does just the opposite. The video begins by comparing Fahrenheit and Celsius. He points out that Fahrenheit measures water to freeze at 32 and water to boil at 212. Celsius measures water to freeze at 0 and water to boil at 100. To convert Celsius to Fahrenheit, multiply the Celsius temperature by 1.8 and add 32. Many countrie...
How To: Sketch the graph of a piecewise function
This video teaches us to draw the graph of a piecewise function. This is shown using two examples. In the first example we have 'y' equal to 'x + 2' for x less than zero and '1 - x' for x greater than equal to zero. We plot two points on the function for x less than zero and do the same for the function with x greater than equal to zero. The graph for the first function is erased for x greater than equal to zero, and the same is done for the second function for x less than zero. Note that the...