On Yay Math, Robert Ahdoot, founder of Yay Math, will show you some square root functions and some inequalities. He begins with the problem y=x². Then he makes a sketch with two intersecting lines in a t shape. The problem is illustrated by a curved U shape, the U's bottom resting on the horizontal bar, which represents x, while the center takes the vertical line. The vertical bar represents y. This U is directed up because the x² is a positive number. If the number were negative, the U would be in the other direction under the horizontal line. In this problem you can take the square from the x and add it to the y like this: y²=x. The second example will have the horizontal line in the center of the U shape and the vertical line at its base, being a positive number it goes to the right, or opens to the right. So positive numbers either open upward or the right. A vertical line should not be able to touch the curved line in two places. In the first diagram, a vertical line (hold a pencil to it) does not touch in more than one place, while in the second example of y²=x, it does. The first example is a function and the second is not. The second equation needs to be made a function, and how to do this is by getting the square root on both sides. This will create y equals the square root of x and on the illustration the U shape will only show on the top half because the y is positive and the square root is minus or negative, which is imagined on the t-diagram. The whole lesson is graphing problems correctly. A square root has a T shape through the curve while other problems are linear in shape when graphed. By setting the variables of a problem to zero, you will get the intercept of the alternate component. With x at 0 you find the y intercept, and with y at 0 you find the x intercept. He solves the equation y = the square root of 3x + 4 here.
Apple's iOS 26 and iPadOS 26 updates are packed with new features, and you can try them before almost everyone else. First, check Gadget Hacks' list of supported iPhone and iPad models, then follow the step-by-step guide to install the iOS/iPadOS 26 beta — no paid developer account required.




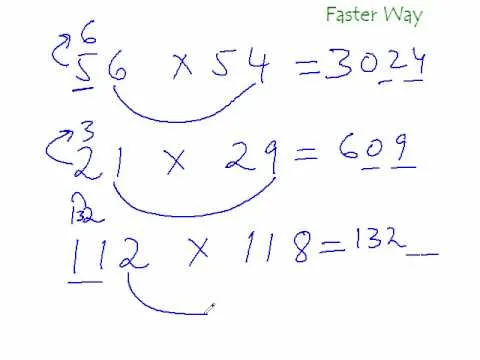
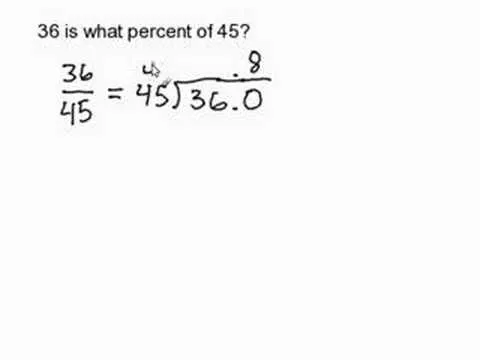












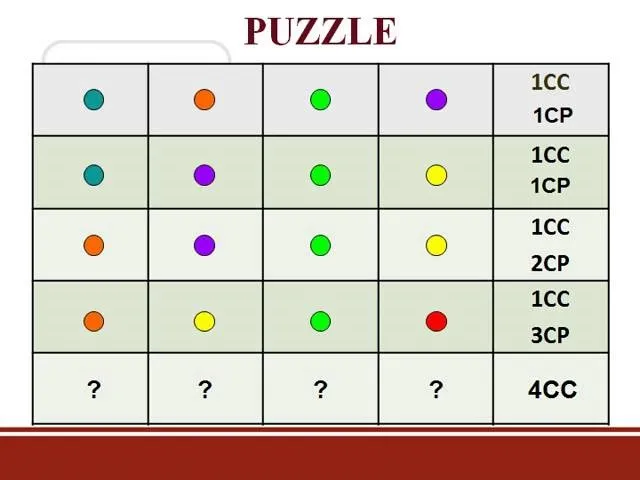





Comments
Be the first, drop a comment!