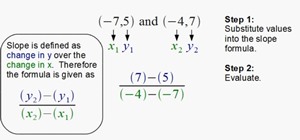
If you've ever been asked to find the GCF, or Greatest Common Factor, of a series of numbers or algebraic expressions, check out this video to learn how.
The methods for finding the greatest common factor for a series of numbers and for an algebraic expression are similar.
Step 1: Determine for a series of numbers
Factor each number in a series of numbers completely into its primes; identify the common factors for each number; and then multiply the common factors together.
TIP: A prime number is a positive integer that is not itself the product of two smaller positive integers.
Step 2: Use 18 and 27
Use the numbers 18 and 27 as an example. The primes of 18 are three, three, and two. The primes of 27 are three, three, and three. So the greatest common factor is three times three, or nine.
Step 3: Determine the greatest common factor for algebraic expressions
Identify all of the common factors in a series of algebraic expressions.
Step 4: factor 60x2y and 210xy2
Use the expressions the common factors of the first expression are two, two, three, five, x, x, and y. The common factors in the second expression are two, three, five, seven, x, y, and y. So the greatest common factor is two times three times five times x times y, or 30xy.
Did you know? The third century B.C.E. mathematician Euclid developed an algorithm for finding the greatest common factor of two natural numbers or two polynomials.
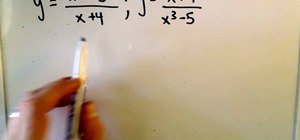
Be the First to Comment
Share Your Thoughts