When a triangle is inserted in a circle in such a way that one of the side of the triangle is diameter of the circle then the triangle is right triangle. To prove this first draw the figure of a circle. Now draw a diameter to it. It can be any line passing through the center of the circle and touching the sides of it. Now making this as the side of a triangle draw two lines from the ends of the diameter to a point on the circle. Now join the center of the circle to the other vertex of the circle dividing the triangle into two smaller equal triangles. Now one angle of the smaller triangle is 90 degrees because the line is perpendicular to the diameter. If you compute the other angle it comes out to be 45. Now the two angles of the smaller triangles make the right angle of the original triangle. This video shows that a triangle inside a circle with one if its side as diameter of circle is right triangle.
Apple's iOS 26 and iPadOS 26 updates are packed with new features, and you can try them before almost everyone else. First, check Gadget Hacks' list of supported iPhone and iPad models, then follow the step-by-step guide to install the iOS/iPadOS 26 beta — no paid developer account required.




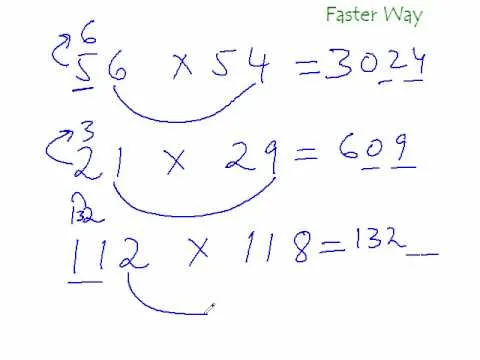
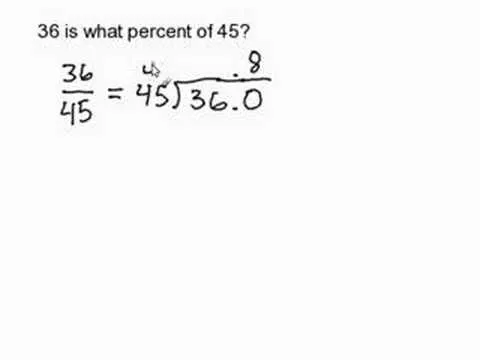












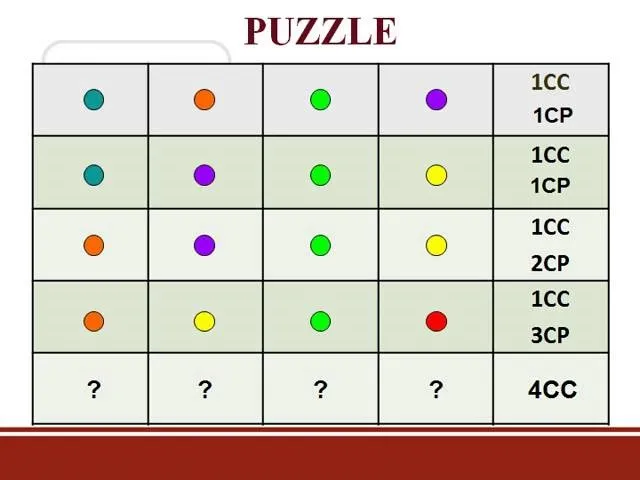





Comments
Be the first, drop a comment!