Apply the Pythagorean Theorem
Today we are going to look at applying the Pythagorean Theorem.
Example problem. A 12 foot ladder is placed four feet from the base of a wall,
how far up the wall will the ladder reach?
Rules of working with a word problems in Geometry.
First rule is that you always draw a picture.
Get out your marker and draw a scenario of what this situation looks like.
Then I want you to label it.
Take all the information and label the picture, and since this is the Pythagorean Theorem.
We will identify where is A where is B and where is C and then we will plug everything into the Pythagorean Theorem, and solve for the unknown.
So let's go through the steps.
Let's draw a picture. We have a wall and we have a ladder leaning against the wall. (Draws this) and now let's label what we know.
We know this is a 12 foot ladder, and it is placed four feet from the base of the wall.
That means my four feet is here. (points to bottom of triangle) and I have the right angle here.
Now opposite the right angle is the hypotenuse or C that means the floor is B so A is missing.
I have now identified A, B, and C.
Apply the Pythagorean Theorem.
So let's square these out, four squared is 16, and 12 squared is 144 ,and I don't know my A squared.
Now, let's subtract 16 from both sides.
To undo a square you take the square root so the square root of 128, so to find the square root of 128
Make a factor tree.
A = 8 is how far up the ladder will reach.
You could also get the decimal version by originally taking the square root of 128 on your calculator, but the exact answer is 8 square 2. Hope this was helpful.
Pythagorean Theorem word problems
 Directions for solving Pythagorean Theorem word problems. Includes many example word problems,and video tutorials
Directions for solving Pythagorean Theorem word problems. Includes many example word problems,and video tutorials






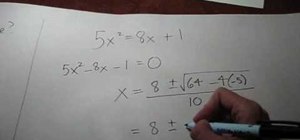











Be the First to Respond
Share Your Thoughts