How-To Guides about Math


how to
How to Calculate Faster Than a Calculator


how to
How to Find the Percent Given Two Numbers


how to
How to Find the Slope Given 2 Ordered Pairs




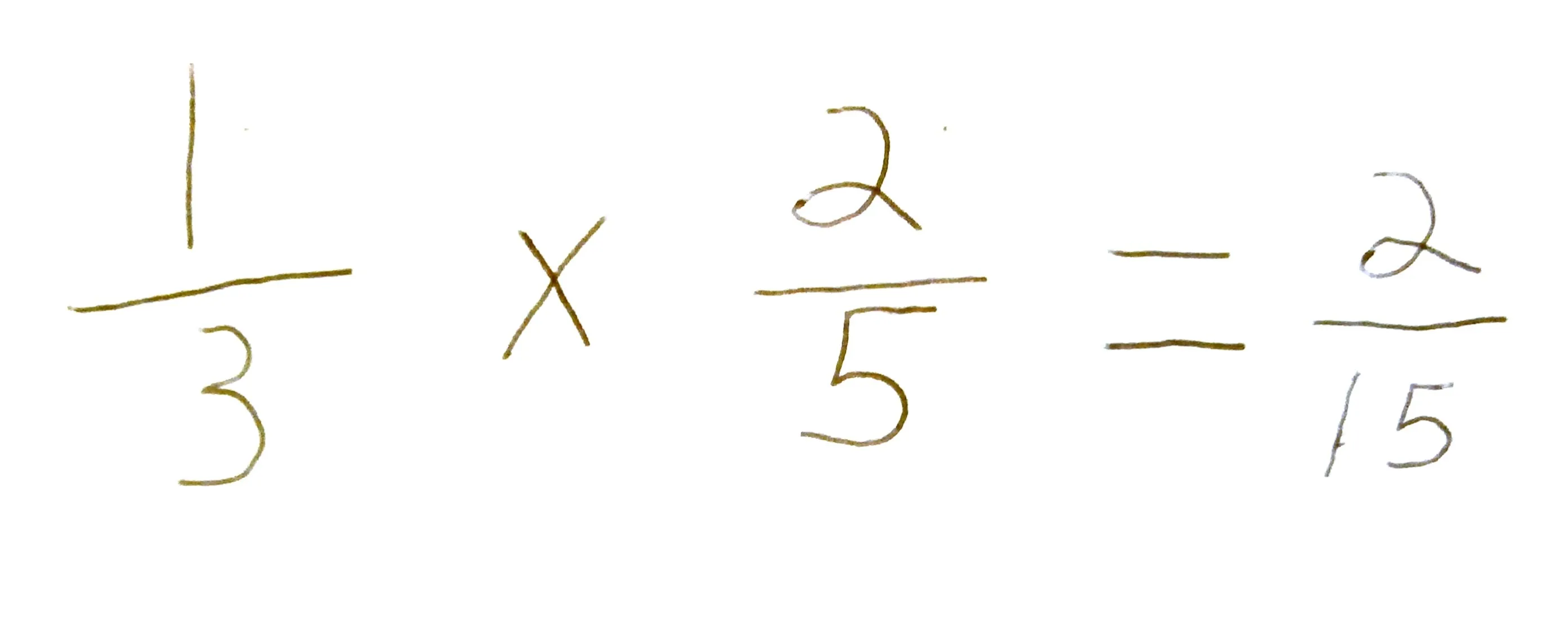


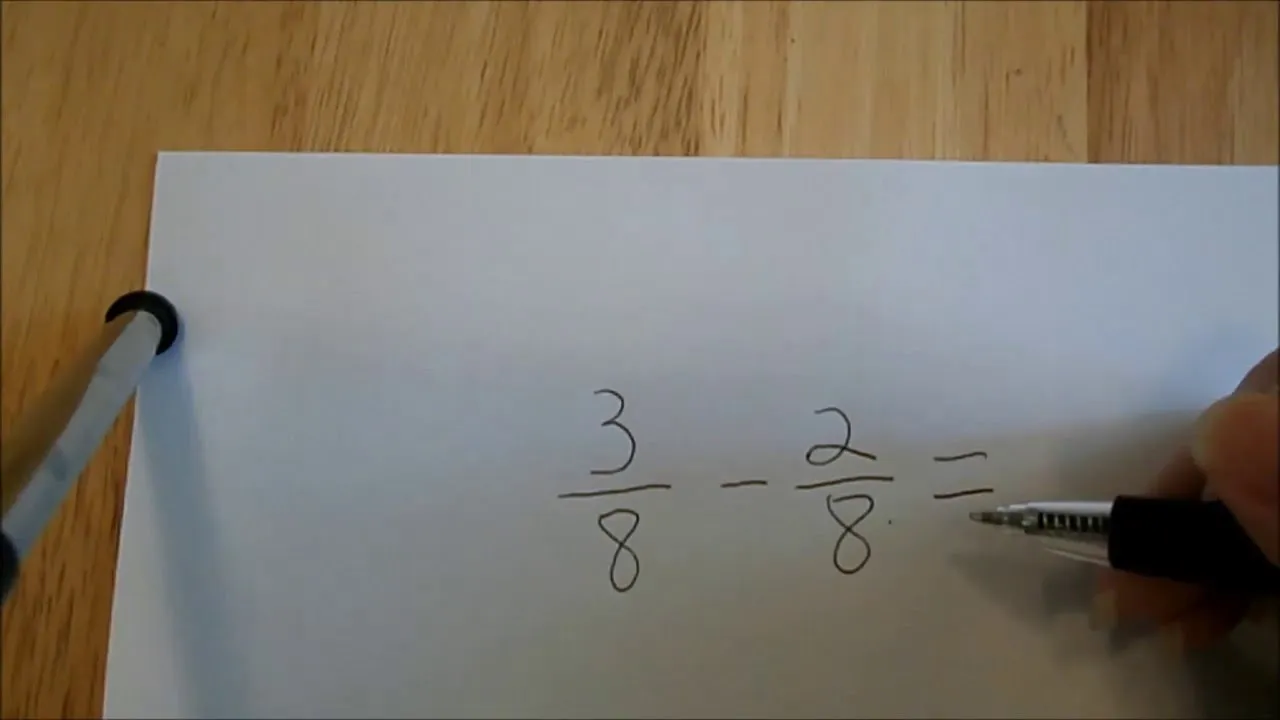






















Featured On WonderHowTo:
Productivity & Shortcuts










Featured On WonderHowTo:
Music & Audio










Featured On WonderHowTo:
Augmented Reality








Featured On WonderHowTo:
Gaming