JustMathTutoring This video shows the procedure of finding derivatives using the Chain Rule. The Chain Rule states that the derivative of a composition of functions is the derivative of the outside function evaluated at the inside multiplied by the derivative of the inside. This can be stated as if h(x) = f[g(x)] then h'(x)=f'[g(x)]g'(x). This is explained by two examples. In the first example we find the derivative of the sine of square of 'x'. We take the derivative of sine at square of 'x' and multiply it with the derivative of the square of 'x'. The second example consists of a function of 'x' raised to the power of 30. This is found by taking the derivative of the power function at the inside function multiplied by the derivative of the inside function.
Apple's iOS 26 and iPadOS 26 updates are packed with new features, and you can try them before almost everyone else. First, check Gadget Hacks' list of supported iPhone and iPad models, then follow the step-by-step guide to install the iOS/iPadOS 26 beta — no paid developer account required.




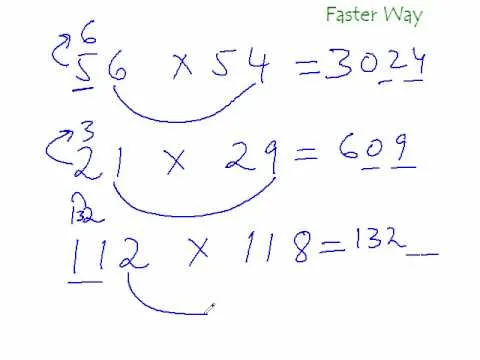
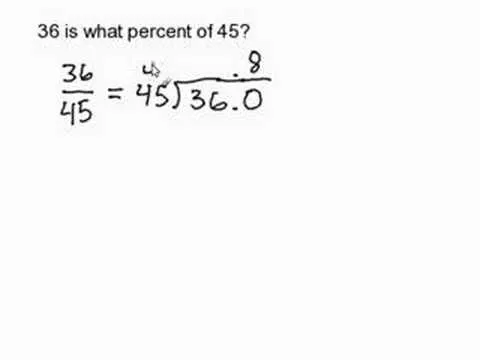












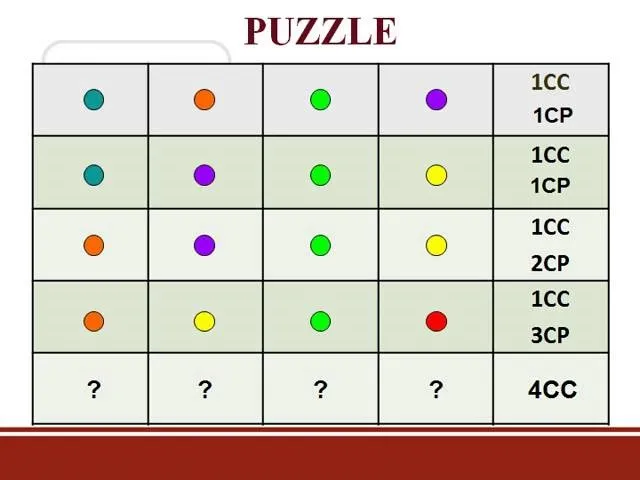





Comments
Be the first, drop a comment!