A conservative vector field is defined as being the gradient of a function, or as a scaler potential. Conservative vector fields are not dependent on the path; they are path independent. Conversely, the path independence of the vector field is measured by how conservative it is. These fields are also characterized as being ir-rotational, which means they have vanishing curls. Actually, ir-rotational vector fields are conservative as long as a certain condition on the geometry of the domain is true: there must be a simple connection.
Want to master Microsoft Excel and take your work-from-home job prospects to the next level? Jump-start your career with our Premium A-to-Z Microsoft Excel Training Bundle from the new Gadget Hacks Shop and get lifetime access to more than 40 hours of Basic to Advanced instruction on functions, formula, tools, and more.
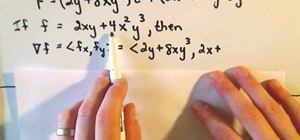
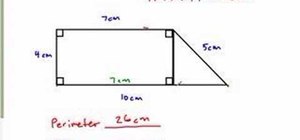
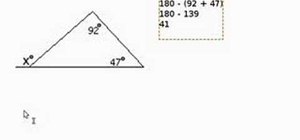
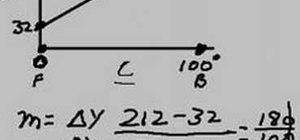
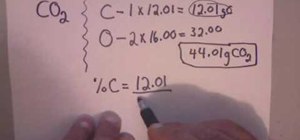
Be the First to Comment
Share Your Thoughts