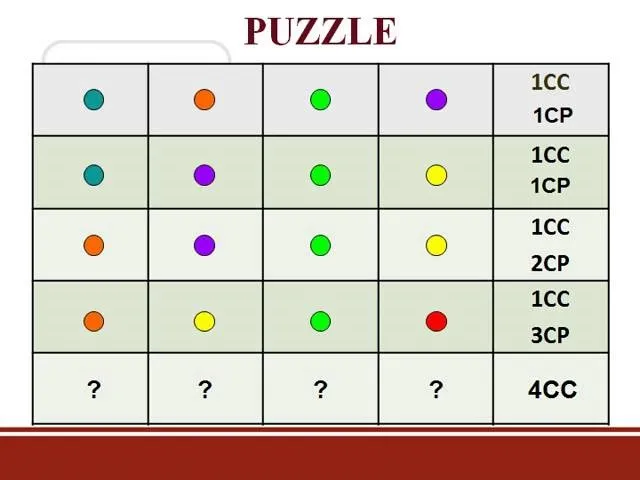
Looking for a guide on how to solve quadratic inequality problems? From Ramanujan to calculus co-creator Gottfried Leibniz, many of the world's best and brightest mathematical minds have belonged to autodidacts. And, thanks to the Internet, it's easier than ever to follow in their footsteps (or just finish your homework or study for that next big test). With this installment from Internet pedagogical superstar Salman Khan's series of free math tutorials, you'll learn how to find the right answers when working with quadratic inequalities in algebra.
Have an iPhone? Check out all 200+ new features coming in iOS 13.
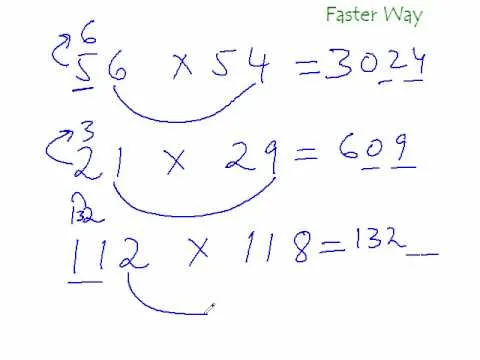
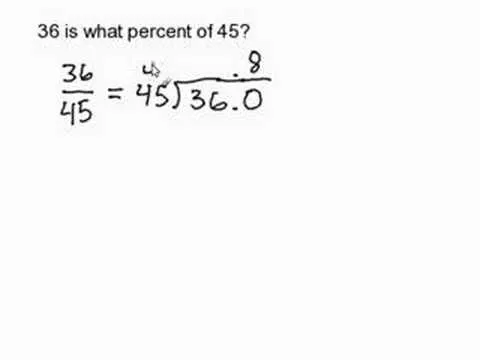
5 Comments
Solving inequalities through factoring as explained in the video may be confused and can not be generalized in case of quadratic inequalities that are in standard form ax^2 + bx + c 0 (or
In general, there are 3 common methods to solve quadratic inequalities:
1. By using the number-line
2. By the algebraic method
3. By graphing.
The simplest way is to use the number-line method. First solve the quadratic equation to get the 2 real roots. Represent these 2 roots on the number-line.
Next use the test-point approach. I advise you to use as test-point the origin x = 0.
Substitute this value x = 0 into the inequality to see if it is true? or not true?
If it is true, then the origin is located on the true segment (the solution set)
If it is not true, then the origin is outside the solution set.
Finally, express the answer in the form of interval. Example: (-2, 7), (-1/3, -7/5] , [ 1, 7]
Share Your Thoughts