This is a great educational video on how to solve quadratic equations by factoring. Let us take an example and try to learn the method. Here is a quadratic equation: (r+7) (r-9) = 0. Consider zero-factor property. For real a and b, if a.b = 0, then a = 0 or b = 0 or both are equal to zero. So r+7 = 0 or r-9 = 0 > r = -7 or r = 9. Hence, r = -7, 9. Similarly to solve a quadratic equation (13r+7) (6r-18) = 0, we will get 13r = -7 or r = -7 over 13. Also 6r = 18 or r = 3. So r= -7over 13, 3. This video will be very useful for the school students.
Just updated your iPhone? You'll find new emoji, enhanced security, podcast transcripts, Apple Cash virtual numbers, and other useful features. There are even new additions hidden within Safari. Find out what's new and changed on your iPhone with the iOS 17.4 update.
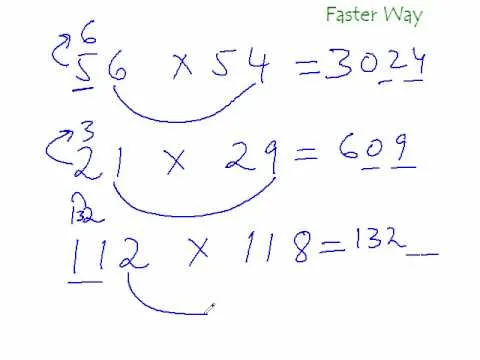
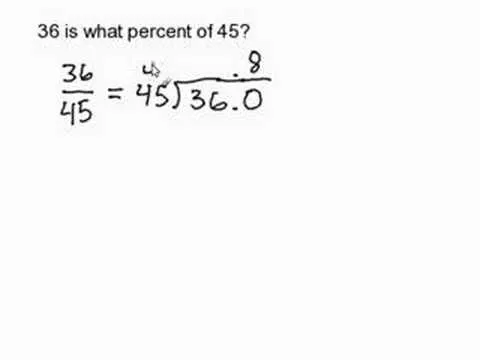
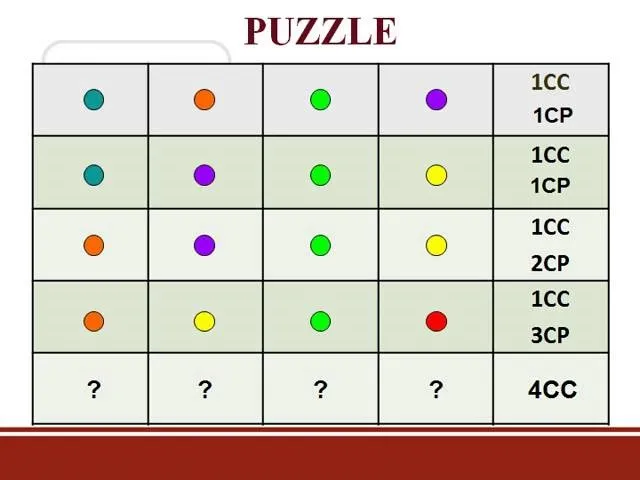
2 Comments
To solve quadratic equations in standard form ax^2 + bx + c = 0 that can be factored, there is a new "Transforming Method" recently introduced on Yahoo or Google Search. This is may be the simplest and fastest method so far. Its strong points are: systematic, no guessing, no factoring by grouping, and no solving binomials. See the articles titled:"Solving quadratic equations by the new Transforming Method" on Yahoo or Google Search.
Solving quadratic equations by the new Transforming Method.
This method proceeds through 3 steps.
STEP 1. Transform the equation ax^2 + bx + c = 0 (1) into the simplified one x^2 + bx + ac = 0 (2), with a = 1, and C = ac.
STEP 2. Solve the transformed equation (2) by the Diagonal Sum Method (Yahoo or Google Search) that immediately obtains the 2 real roots y1 and y2 of equation (2).
STEP 3. Divide both y1 and y2 by the coefficient a to get the 2 real roots x1 and x2 of the original equation (1): x1 = y1/a, and x2 = y2/a.
Example. Solve: 24x62 + 59x + 36 = 0 (1). Transformed equation: x^2 = 59x + 864. (2). Both roots are negative (recall the Rule of Signs for Real Roots). Compose factor pairs of ac = 864 with all negative numbers. To save time, start from the middle of the factor chain. Proceeding: .....(-18, -48)(-24, -36)(-27, -32). This last sum is -27 - 32 = -59 = -b. Then, the 2 real roots of (2) are y1 = -27 and y2 = -32. Back to the original equation (1), the 2 real roots are: x1 = y1/24 = -27/24 = -9/8,, and x2 = y2/24 = -32/24 = -4/3.
Share Your Thoughts