The video shows how to solved mixed property problems using the exponent rules. See if there are any rules you can apply to the problem until you get to a point where you can't simplify anymore. The instructor shows in the example problem that the two bases are the same, but there is extras happening the numerator. The power to power multiply rule is applied removing the extra issues from the numerator. Next the quotient rules is applied as there is the exact same base to the power so we keep the base and subtract the powers. Leaving the expression simplified. Next the problem has same bases, same bases being multiplied you add the exponents to simplify. However if there is a negative exponent in the answer it should be shifted down to be below 1. In the next solution the numerator is very complex so should be simplified first, the rule used is exponents distribute over location so each base has the power applied. Once the parenthesis are removed then the quotient rule can be used again which simplifies the expression. In the final example, there are parenthesis and these should be removed. Distribute the outside exponent to the inside, giving it to both the numerator and the denominator. Next look for same bases but there aren't any so just get rid of negative exponents. Move the negative expression up or down depending on their location. Simplify the numerical exponents into one single integer.
Apple's iOS 26 and iPadOS 26 updates are packed with new features, and you can try them before almost everyone else. First, check Gadget Hacks' list of supported iPhone and iPad models, then follow the step-by-step guide to install the iOS/iPadOS 26 beta — no paid developer account required.




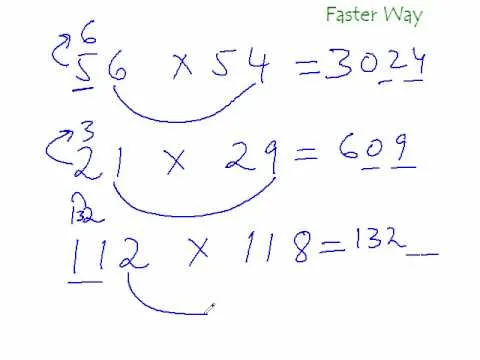
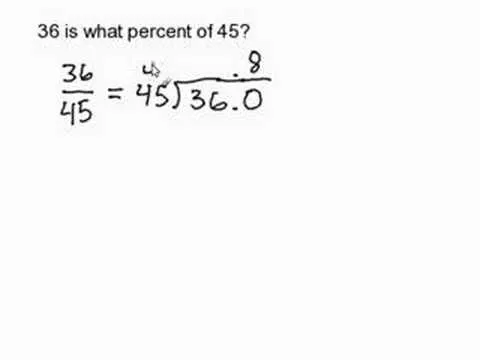

















Comments
Be the first, drop a comment!