Most of the time, when I'm bored during math class, I play with my calculator to satisfy my boredom. Recently, I've discovered that when multiplying any number by 11, 111, or any number similar to it, that it has a pattern (though I guess everything in math has a pattern). I don't know if this technique is original, because I didn't read anything about this. It's just mere observation. If it's a tried and true technique, let me know.
Basic Multiplication
The basic form in multiplication is A x B = C.
Where A is the multiplicand, B is the multiplier, and C is the product.
Multiplying Single Digit Multiplicands
We all know that when we multiply a number lower than 10 by 11, we just copy the multiplicand base (1-9) onto the number of 1's in the multiplier (11, 111, 1,111, and so on).
Examples:
- 2 x 11 = 22
- 4 x 111 = 444
Multiplying Multiplicands with Two or More Digits by 11
When multiplying any multiplicand by 11, it is just as easy as multiplying with a single digit multiplicand.
Divide the Multiplicand into Two Parts
When I say divide the multiplicand into two parts, I don't mean mathematically divide it by 2 (which is A/2). I mean separate the two digits, which will be named A and B.
Let's use the problem 56 x 11 = ? for our example in this article.
56 x 11 = ?
Separate the multiplicand into two parts.
5 | 6
Now 56 is separated into two parts—5 and 6.
A = 5 and B= 6
B Is the Last Digit of the Product
In the first step, we divided the multiplicand into two separate digits to get A and B. The last digit of the product (the ones place) will be B.
A =5 and B =6
6 will now be the last digit (ones) in the product.
56 x 11 = __6
Sum of A and B Is the Middle Digit
To get the middle portion of the product (the tens), find the sum of A and B, as in C. But only the last digit (the ones) in C is considered. The rest is carried over.
Find the sum of A and B.
A + B = ?
Since A is 5 and B is 6, we get the equation: A + B = C => 5 + 6 = ? => 5 + 6 = 11.
Since only the last digit (the ones) is considered in C for the final product...
56 x 11 = _16
The tens (1) is carried over.
First Digit(s) of the Product
To find the first digit/s of the product, add A with the carried over number from the previous step.
Now, the first digit (hundreds) of the final product is A, added to it the number carried over from the tens of the last step (1).
56 x 11 = (5+1)16
Which amounts to...
56 x 11 = 616
Until Next Time
I wanted to write everything in just one article, but realize that it would be too long. Don't forget to subscribe and like if you learned something, and also don't hesitate to ask anything regarding the topic.




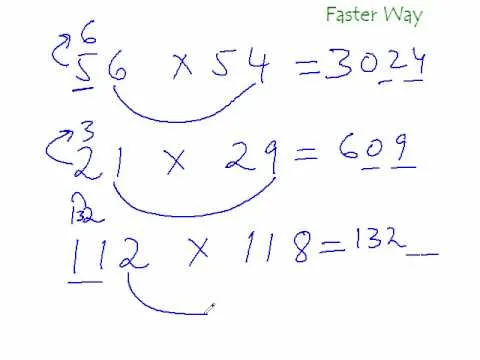

















Comments
Be the first, drop a comment!