It doesn't matter how long ago your last geometry class was, you can still impress your friends by finding a geometric mean. The geometric mean can be used to find the average of numbers with out unusually high or low results effecting the result.
The geometric mean of two numbers is the square root of their product. More generally, it is the "nth" root of the product of n numbers.
You Will Need
* A set of numbers
* A calculator with advanced math functions
Step 1: Take the square root for two numbers
Take the square root of the product if you are only dealing with two numbers. This is the geometric mean when there are only two numbers.
The geometric mean of 2 and 72 is the square root of their product, or 12.
Step 2: Determine logarithms for more than two numbers
If you are dealing with more than two numbers, determine the logarithm of each number that will be multiplied. Use the logarithmic function key on your calculator to calculate these values.
Step 3: Add the values
Add each of these logarithmic values together.
Step 4: Divide by the number of values
Divide the sum of the logarithmic values by the total number of values.
Step 5: Determine the antilog value
Determine the antilog value of the average using the antilogarithm function key on your calculator. This is the geometric mean for the general case.
Health inspectors often report bacteria concentrations at public beaches as geometric means so that very high or very low numbers don't skew the average.





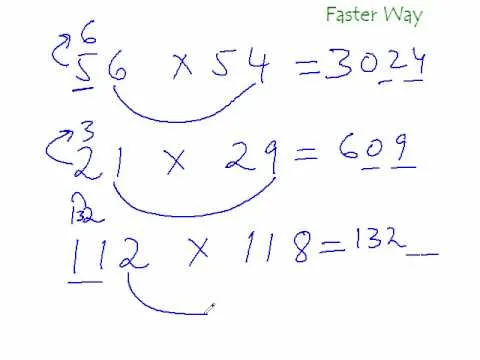
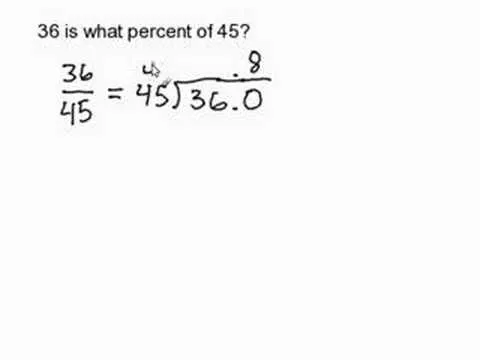

















Comments
Be the first, drop a comment!