The relationship and the definition of derivatives and anti-derivatives is described in this video. First, consider a function F(x)=x^3-5x+2 and another with small 'f', f(x)=3x-5. f(x) here is the derivative of F(x). However, on the contrary, F(x) is said to be the anti-derivative of f(x). There is a catch though; even though F(x) has only one derivative in the form of f(x), f(x) here has more than one anti-derivative. This is because f(x)'s anti-derivatives are of the form F(x)=x^3-5x+c, where c stands for any constant number. For example, f(x) anti-derivatives can be any of the following: F(x)=x^3-5x+2, F(x)=x^3-5x, F(x)=x^3-5x+4... and so on.
Apple's iOS 26 and iPadOS 26 updates are packed with new features, and you can try them before almost everyone else. First, check Gadget Hacks' list of supported iPhone and iPad models, then follow the step-by-step guide to install the iOS/iPadOS 26 beta — no paid developer account required.




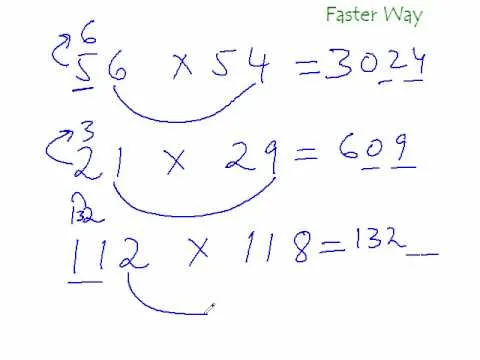
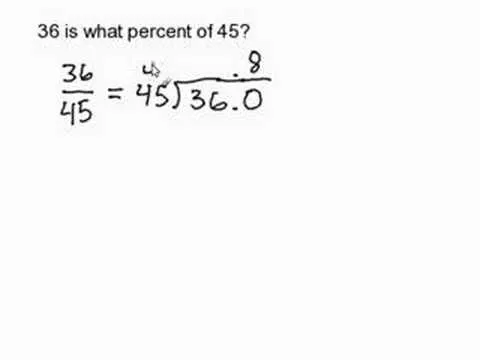












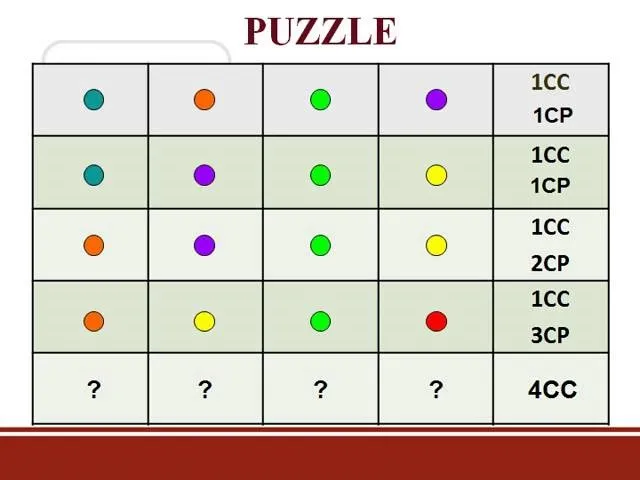





Comments
Be the first, drop a comment!