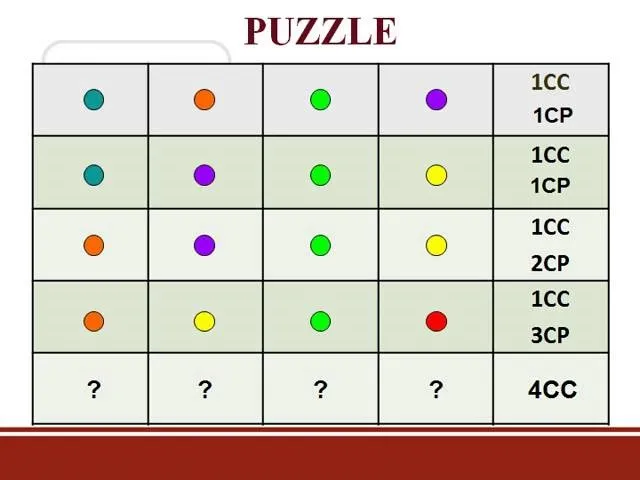
This video explains how to solve the problem of probability dependent events. In this video the problem is that a box contains three pens, 2 markers, and 1 highlighter. The person selects one item at random and does not return it to the box. So what is the probability that the person selects 1 pen and 1 marker. That is 6 items total. First she count the all items that involved in this problem. Then count the individual probability of the pen and marker. The person selects 3 pens out of 6 items so the probability is 3/6. Out of three pens she fix with a pen so the number of pens goes down to 2. She did not pick a marker so it is 2 out of 2. She does not take the highlighter too. So total is 5. Next take the markers probability is out of 2 markers in the 5 items is 2/5. Next calculate combined probability by combined the pen and marker probability. That is 3/6 x 2/5. So it is equal to 6/30. That is the way described in this video that how to calculate the probability dependent events.
Apple's iOS 26 and iPadOS 26 updates are packed with new features, and you can try them before almost everyone else. First, check Gadget Hacks' list of supported iPhone and iPad models, then follow the step-by-step guide to install the iOS/iPadOS 26 beta — no paid developer account required.




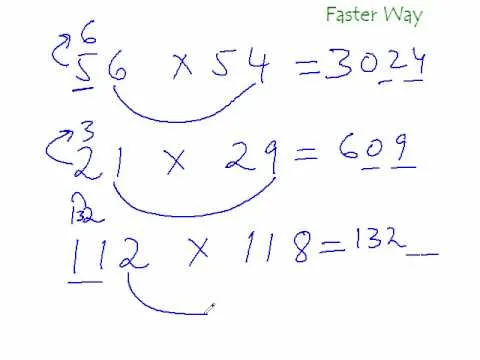
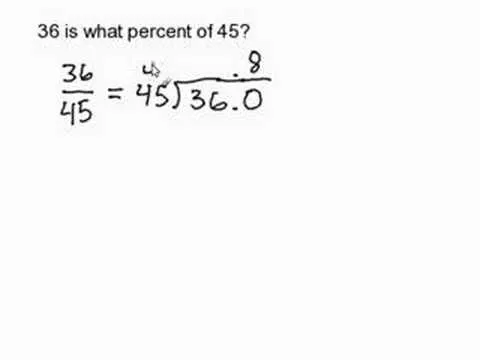

















Comments
Be the first, drop a comment!