The idea of finding the area under a curve is an important fundamental concept in calculus. Consider a function y = f(x). Now the area under the curve is to be calculated. The area under a curve problem is stated as 'Let f(x) be non negative on [a, b]. Find the area of the region lying beneath the curve y = f(x) and above the x-axes, from x = a to x = b. Note that finding the area under a curve will imply that you are dealing with a non negative function. The way to approach is to divide the entire interval between a and b into sub intervals there by construction small rectangles side by side. Now the area under the curve can be approximated as the sum of the areas of the individual rectangles. The smaller the width of the rectangles the more precise your final answer will be. This video shows how to approximate the area under a curve using rectangles.
Apple's iOS 26 and iPadOS 26 updates are packed with new features, and you can try them before almost everyone else. First, check Gadget Hacks' list of supported iPhone and iPad models, then follow the step-by-step guide to install the iOS/iPadOS 26 beta — no paid developer account required.




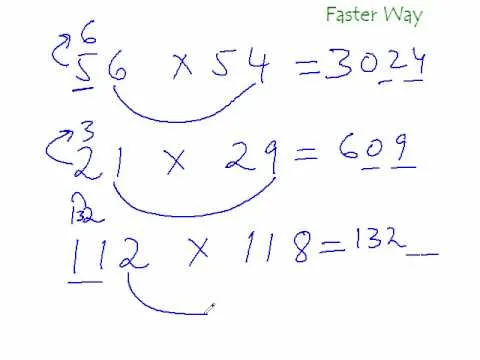
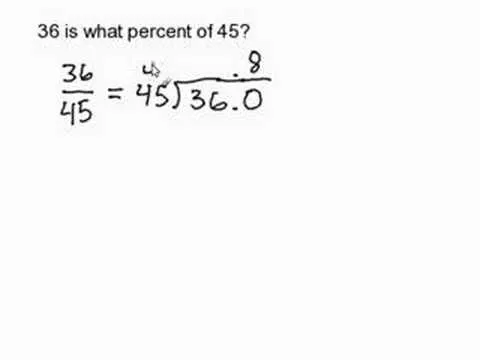












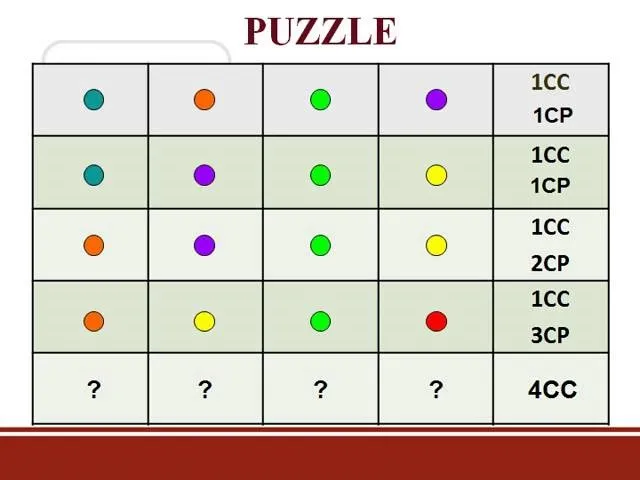





Comments
Be the first, drop a comment!