In this video you will learn how to solve basic one step equations that contain fractions.
The video contains two examples in which you have to divide the fractions, and one in which you multiply the fractions.
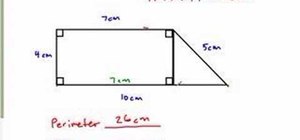
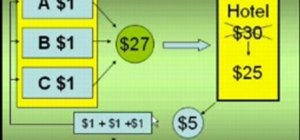
For more one step equations see.....
Forum Thread:
How to Use Slope Intercept Form
1
Replies
Forum Thread:
How to Find the Radius of a Sphere Given the Volume
1
Replies
Forum Thread:
How to Calculate the Volume,Radius, and the Diameter of a Sphere Given the Area
0
Replies
Forum Thread:
How to Solve Order of Operation Problems.
0
Replies
Forum Thread:
How to Multiply and Divide Fractions
0
Replies
Forum Thread:
How to Solve One Step Equations
0
Replies
Forum Thread:
How to Change a Quadratic Equation from Standard Form to Vertex Form
0
Replies
Forum Thread:
How to Subtract Integers
0
Replies
Forum Thread:
How to Solve Unit Rate Problems
0
Replies
Forum Thread:
How to Find an Outlier in Math
0
Replies
Forum Thread:
How to Add and Subtract Integers
0
Replies
Forum Thread:
How to Identify the Faces, Edges, and Vertices of a 3D Shape
0
Replies
Forum Thread:
Do You Think Elementary School Kids Could Solve This Type of Question ??
0
Replies
Forum Thread:
How to Solve Basic Two Step Equations
0
Replies
Forum Thread:
How to Study for School
0
Replies
Forum Thread:
How to Calculate Percentage Change
0
Replies
Forum Thread:
How to Convert a Decimal to a Fraction
0
Replies
Forum Thread:
How to Determine if Data Is Discrete or Continuous
0
Replies
Forum Thread:
How to Tell if a Number Is Rational and Irrational Number
0
Replies
Forum Thread:
How to Convert Meters to Feet and Kilometers to Miles
0
Replies
How To:
Simplify a quadratic formula result
How To:
Calculate Faster Than a Calculator
How To:
Find the circumference of a circle
How To:
Find the slope of a line given 2 points with fractions
How To:
Find a slope of a straight line with: Ax + By + C = 0
How To:
Solve linear equations in the form of AX+B=C
How To:
Simplify radical expressions
How To:
Figure out and calculate sales tax
How To:
Find the volume of a cylinder
How To:
Learn Calculus in 20 minutes
How To:
Use ">" (greater than) and "<" (less than) symbols
How To:
Multiply & Divide Numbers (Basic Elementary Math)
How To:
Subtract a mixed number from a proper fraction in basic math
How To:
Find the Slope Given 2 Ordered Pairs
How To:
Find extra points for a parabola (quadractic equation)
How To:
Find Leg Lengths and Hypotenuse of a 45 45 90 Triangle
How To:
Solve word problems involving direct variation
How To:
Solve a word problem that involves proportions
How To:
Find the equation of a line given 2 points
How To:
Find the perimeter & area of a complex figure
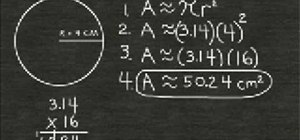
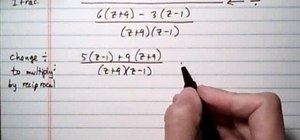
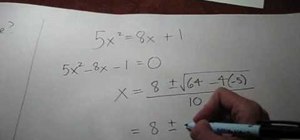
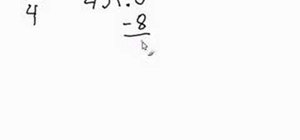
Be the First to Respond
Share Your Thoughts